geometry problems from All-Ukrainian Correspodence MO for grades 5-12 (years 1996 -2016 by magazine ''In the World of Mathematics''' ) with aops links
Всеукраїнська заочна математична олімпіада
collected inside aops here
all problems in Ukrainian here
2003 - 2021
looking for 8 first rounds (1996-2002), I-VII
Let $O$ be the center of the circle $\omega$, and let $A$ be a point inside this circle, different from $O$. Find all points $P$ on the circle $\omega$ for which the angle $\angle OPA$ acquires the greatest value.
In the triangle $ABC$, $D$ is the midpoint of $AB$, and $E$ is the point on the side $BC$, for which $CE = \frac13 BC$. It is known that $\angle ADC =\angle BAE$. Find $\angle BAC$.
Let $ABCDEF$ be a convex hexagon, $P, Q, R$ be the intersection points of $AB$ and $EF$, $EF$ and $CD$, $CD$ and $AB$. $S, T,UV$ are the intersection points of $BC$ and $DE$, $DE$ and $FA$, $FA$ and $BC$, respectively. Prove that if $ \frac{AB}{PR}=\frac{CD}{RQ}=\frac{EF}{QP},$ then $\frac{BC}{US}=\frac{DE}{ST}=\frac{FA}{TU}.$
$6$ apple trees grow in the garden. Could it be that among any three apple trees, one is at the same distance from the other two?
A circle is drawn on the plane. How to use only a ruler to draw a perpendicular from a given point outside the circle to a given line passing through the center of this circle?
The extensions of the sides $AB$ and $CD$ of the trapezoid $ABCD$ intersect at point $E$. Denote by $H$ and $G$ the midpoints of $BD$ and $AC$. Find the ratio of the area $AEGH$ to the area $ABCD$.
In an isosceles triangle $ABC$ ($AB = AC$), the bisector of the angle $B$ intersects $AC$ at point $D$ such that $BC = BD + AD$. Find $\angle A$.
An equilateral triangle with side $8$ is divided into equilateral triangles with side $1$. What is the largest number of these triangles that can be colored so that no two colored triangles have common vertices?
The bisectors of the angles $A$ and $B$ of the triangle $ABC$ intersect the sides $BC$ and $AC$ at points $D$ and $E$. It is known that $AE + BD = AB$. Find the angle $\angle C$.
Let $O$ be the point of intersection of the diagonals of the trapezoid $ABCD$ with the bases $AB$ and $CD$. It is known that $\angle AOB = \angle DAB = 90^o$. On the sides $AD$ and $BC$ take the points $E$ and $F$ so that $EF\parallel AB$ and $EF = AD$. Find the angle $\angle AOE$.
Let the circle $\omega$ be circumscribed around the triangle $\vartriangle ABC$ with right angle $\angle A$. Tangent to the circle $\omega$ at point $A$ intersects the line $BC$ at point $D$. Point $E$ is symmetric to $A$ with respect to the line $BC$. Let $K$ be the foot of the perpendicular drawn from point $A$ on $BE$, $L$ the midpoint of $AK$. The line $BL$ intersects the circle $\omega$ for the second time at the point $N$. Prove that the line $BD$ is tangent to the circle circumscribed around the triangle $\vartriangle ADM$.
Find the locus of the points of intersection of the othocenters of the triangles inscribed in a given circle.
Mark $101$ points on the plane, none of which are not lie on one line and none of the four lie on the same circle. Prove that there is a circle that passes through three of these points and for which exactly $49$ marked points lie inside and exactly $49$ outside.
Let $D$ and $E$ be the midpoints of the sides $BC$ and $AC$ of a right triangle $ABC$. Prove that if $\angle CAD=\angle ABE$, then$$\frac{5}{6} \le \frac{AD}{AB}\le \frac{\sqrt{73}}{10}.$$
Let $ABC$ be an isosceles triangle ($AB=AC$). An arbitrary point $M$ is chosen on the extension of the $BC$ beyond point $B$. Prove that the sum of the radius of the circle inscribed in the triangle $AMB$ and the radius of the circle tangent to the side $AC$ and the extensions of the sides $AM, CM$ of the triangle $AMC$ does not depend on the choice of point $M$.
The vertices of a regular $1000$-gon are painted red, blue and yellow. In one step, you can select two adjacent vertices of different colors and repaint them with a third color. Is it always possible to get a polygon in a few such steps, all vertices of which have a common color?
Is it possible to draw a pentagon on plaid paper with the side of cell $1$ so that all its vertices lie in the nodes of the grid, and the product of the lengths of all sides and the product of the lengths of all diagonals are integers?
Let $ABC$ be an isosceles triangle ($AB = AC$), $D$ be the midpoint of $BC$, and $M$ be the midpoint of $AD$. On the segment $BM$ take a point $N$ such that $\angle BND = 90^o$. Find the angle $ANC$.
In triangle $ABC$, the lengths of all sides are integers, $\angle B=2 \angle A$ and $\angle C> 90^o$. Find the smallest possible perimeter of this triangle.
Denote by $B_1$ and $C_1$, the midpoints of the sides $AB$ and $AC$ of the triangle $ABC$. Let the circles circumscribed around the triangles $ABC_1$ and $AB_1C$ intersect at points $A$ and $P$, and let the line $AP$ intersect the circle circumscribed around the triangle $ABC$ at points $A$ and $Q$. Find the ratio $\frac{AQ}{AP}$.
Tom made two rectangles of $2 \times 6$ and $7 \times 8$ from several rectangular tiles measuring $1 \times 3$ and $1 \times 4$, but Jerry snatched and hid one tile from each of the rectangles. Will Tom be able to make a $5 \times 12$ rectangle from the remaining tiles?
What is the largest $n$ such that exists a $n$-gon, in which two adjacent sides have length $1$, and all diagonals have integer lengths?
On the sides $AC$ and $AB$ of the triangle $ABC$, the points $D$ and $E$ were chosen such that $\angle ABD =\angle CBD$ and $3 \angle ACE = 2\angle BCE$. Let $H$ be the point of intersection of $BD$ and $CE$, and $CD = DE = CH$. Find the angles of triangle $ABC$.
Let $ABCD$ be a parallelogram. A circle with diameter $AC$ intersects line $BD$ at points $P$ and $Q$. The perpendicular on $AC$ passing through point $C$, intersects lines $AB$ and $AD$ at points $X$ and $Y$, respectively. Prove that the points $P, Q, X$ and $Y$ lie on the same circle.
A maze is an $8\times 8$ chessboard with walls between some cells so that you can go from one cell to another. By the command "$\uparrow$", "$\downarrow$ "," $\rightarrow$ "or" $\leftarrow$" the hobbit, which is in one of the cells, moves one cell down, up, left or right, if it does not bump into the wall or edge of the board. Otherwise, it remains in place. Gandalf writes a program that consists only of the commands $\uparrow$", "$\downarrow$ "," $\rightarrow$ " and " $\leftarrow$" and passes it to Saruman, who builds a maze, selects the starting cell for the hobbit and forces him to run the program. Can Gandalf guarantee that by following his program, the hobbit will visit all the cells of the chessboard?
A right triangle is drawn on the plane. How to use only a compass to mark two points, such that the distance between them is equal to the diameter of the circle inscribed in this triangle?
Let $ABCDE$ be a convex pentagon such that $AE\parallel BC$ and $\angle ADE = \angle BDC$. The diagonals $AC$ and $BE$ intersect at point $F$. Prove that $\angle CBD= \angle ADF$.
The equilateral triangle $ABC$ is divided into $100$ equal equilateral triangles. Is it possible to mark $8$ vertices of small triangles so that no segment with ends at the marked points is parallel to any side of triangle $ABC$?
In triangle $ABC$, the length of the angle bisector $AD$ is $\sqrt{BD \cdot CD}$. Find the angles of the triangle $ABC$, if $\angle ADB = 45^o$.
Prove that for every $n\ge 4$ there is a hexagon that can be cut into $n$ identical triangles.
An arbitrary point $D$ was marked on the median $BM$ of the triangle $ABC$. It is known that the point $DE\parallel AB$ and $CE \parallel BM$. Prove that $BE = AD$
Let $ABC$ be an acute-angled triangle in which $\angle BAC = 60^o$ and $AB> AC$. Let $H$ and $I$ denote the points of intersection of the altitudes and angle bisectors of this triangle, respectively. Find the ratio $\angle ABC: \angle AHI$.
The kid cut out of grid paper with the side of the cell $1$ rectangle along the grid lines and calculated its area and perimeter. Carlson snatched his scissors and cut out of this rectangle along the lines of the grid a square adjacent to the boundary of the rectangle.
- My rectangle ... - kid sobbed. - There is something strange about this figure!
- Nonsense, do not mention it - Carlson said - waving his hand carelessly. - Here you see, in this figure the perimeter is the same as the area of the rectangle was, and the area is the same as was the perimeter!
What size square did Carlson cut out?
Let $ABCD$ be a trapezoid in which $AB \parallel CD$ and $AB = 2CD$. A line $\ell$ perpendicular to $CD$ was drawn through point $C$. A circle with center at point $D$ and radius $DA$ intersects line $\ell$ at points $P$ and $Q$. Prove that $AP \perp BQ$.
On the diagonals $AC$ and $CE$ of a regular hexagon $ABCDEF$ with side $1$ we mark points$ M$ and $N$ such that $AM = CN = a$. Find $a$ if the points $B, M, N$ lie on the same line.
In a quadrilateral $ABCD$, the diagonals are perpendicular and intersect at the point $S$. Let $K, L, M$, and $N$ be points symmetric to $S$ with respect to the lines $AB, BC, CD$, and $DA$, respectively, $BN$ intersects the circumcircle of the triangle $SKN$ at point $E$, and $BM$ intersects described the circle of the triangle $SLM$ at the point $F$. Prove that the quadrilateral $EFLK$ is cyclic .
Can a square be cut into a triangle, quadrilateral, pentagon, and hexagon (not necessarily convex) such that none of these polygons has right angles?
Beetles sit on the nodes of the $3 \times 100$ grid ($100$ beetles in each row and $3$ beetles in each column). How many straight lines can be drawn on which exactly $3$ beetles sit?
Let $O$ and $H$ be the center of the circumcircle and the point of intersection of the altitudes of the acute triangle $ABC$ respectively, $D$ be the foot of the altitude drawn to $BC$, and $E$ be the midpoint of $AO$. Prove that the circumcircle of the triangle $ADE$ passes through the midpoint of the segment $OH$.
The diagonals $AC$ and $BD$ of the cyclic quadrilateral $ABCD$ intersect at a point O. It is known that $\angle BAD = 60^o$ and $AO = 3OC$. Prove that the sum of some two sides of a quadrilateral is equal to the sum of the other two sides.
An arbitrary point $D$ is marked on the hypotenuse $AB$ of a right triangle $ABC$. The circle circumscribed around the triangle $ACD$ intersects the line $BC$ at the point $E$ for the second time, and the circle circumscribed around the triangle $BCD$ intersects the line $AC$ for the second time at the point $F$. Prove that the line $EF$ passes through the point $D$.
Given $11$ rectangles of different sizes, all sides of which are integral and do not exceed $10$. Prove that there are three of these rectangles, that the first can be placed inside the second, and the second can be placed inside the third.
Let $E$ be the point of intersection of the diagonals of the cyclic quadrilateral $ABCD$, and let $K, L, M$ and $N$ be the midpoints of the sides $AB, BC, CD$ and $DA$, respectively. Prove that the radii of the circles circumscribed around the triangles $KLE$ and $MNE$ are equal.
Given a triangle $ABC$. The circle $\omega_1$ passes through the vertex $B$ and touches the side $AC$ at the point $A$, and the circle $\omega_2$ passes through the vertex $C$ and touches the side $AB$ at the point $A$. The circles $\omega_1$ and $\omega_2$ intersect a second time at the point $D$. The line $AD$ intersects the circumcircle of the triangle $ABC$ at point $E$. Prove that $D$ is the midpoint of $AE$.
Krut and Vert go by car from point $A$ to point $B$. The car leaves $A$ in the direction of $B$, but every $3$ km of the road Krut turns $90^o$ to the left, and every $7$ km of the road Vert turns $90^o$ to the right ( if they try to turn at the same time, the car continues to go in the same direction). Will Krut and Vert be able to get to $B$ if the distance between $A$ and $B$ is $100$ km?
Is it possible to cut a rectangle with sides $1$ and $4$ into four parts and fold of them a new rectangle in which one side is twice as long as the other?
Let $ABC$ be an isosceles triangle ($AB = AC$). The points $D$ and $E$ were marked on the ray $AC$ so that $AC = 2AD$ and $AE = 2AC$. Prove that $BC$ is the bisector of the angle $\angle DBE$.
In the triangle $ABC$, it is known that $AC <AB$. Let $\ell$ be tangent to the circumcircle of triangle $ABC$ drawn at point $A$. A circle with center $A$ and radius $AC$ intersects segment $AB$ at point $D$, and line $\ell$ at points $E$ and $F$. Prove that one of the lines $DE$ and $DF$ passes through the center inscribed circle of triangle $ABC$.
Let $\omega$ be the circumscribed circle of triangle $ABC$, and let $\omega'$ 'be the circle tangent to the side $BC$ and the extensions of the sides $AB$ and $AC$. The common tangents to the circles $\omega$ and $\omega'$ intersect the line $BC$ at points $D$ and $E$. Prove that $\angle BAD = \angle CAE$.
Is it possible to place four triangles on the plane so that inside each triangle was exactly one vertex of the other three triangles?
On the sides $BC, AC$ and $AB$ of the equilateral triangle $ABC$ mark the points $D, E$ and $F$ so that $\angle AEF = \angle FDB$ and $\angle AFE = \angle EDC$. Prove that $DA$ is the bisector of the angle $EDF$.
Let $ABC$ be an non- isosceles triangle, $H_a$, $H_b$, and $H_c$ be the feet of the altitudes drawn from the vertices $A, B$, and $C$, respectively, and $M_a$, $M_b$, and $M_c$ be the midpoints of the sides $BC$, $CA$, and $AB$, respectively. The circumscribed circles of triangles $AH_bH_c$ and $AM_bM_c$ intersect for second time at point $A'$. The circumscribed circles of triangles $BH_cH_a$ and $BM_cM_a$ intersect for second time at point $B'$. The circumscribed circles of triangles $CH_aH_b$ and $CM_aM_b$ intersect for second time at point $C'$. Prove that points $A', B'$ and $C'$ lie on the same line.
We say that two triangles are [i]similar[/i] if they are both acute, both right, or both obtuse. In the
vertices of a regular $n$-gon ($n\ge 3$) sat $n$ sparrows, one in each vertex. Then they flew into the
air and again sat on the vertices of this $n$-gon, one at each vertex, but possibly in a different order.
Which n is sure to find three sparrows that sat in the vertices of similar triangles before and after the
flight?
Four congurent triangles are placed on the plane so that every two triangles have two common vertices. Will there be a vertex that is common to all four triangles?
In some cells of the table $n x n$, $n\ge 2$ there are sitting fireflies. Each firefly illuminates all the cells of the row and column in which it is located (including the cell in which it sits). In each cell of the table recorded the number of fireflies that illuminate it. At which n can it happen that the numbers on each of the diagonals are not repeated?
The circle $\omega$ inscribed in an isosceles triangle $ABC$ ($AC = BC$) touches the side $BC$ at point $D$ .On the extensions of the segment $AB$ beyond points $A$ and $B$, respectively mark the points $K$ and $L$ so that $AK = BL$, The lines $KD$ and $LD$ intersect the circle $\omega$ for second time at points $G$ and $H$, respectively. Prove that point $A$ belongs to the line $GH$.
A triangle, a line and three rectangles are located on a plane so that one of the sides of each rectangle is parallel to this line and the rectangles completely cover all sides of the triangle. Prove that the rectangles cover the whole triangle.
Inside the square $ABCD$ mark the point $P$, for which $\angle BAP = 30^o$ and $\angle BCP = 15^o$. The point $Q$ was chosen so that $APCQ$ is an isosceles trapezoid ($PC\parallel AQ$). Find the angles of the triangle $CAM$, where $M$ is the midpoint of $PQ$.
A $5 \times 12$ chocolate bar consists of $30$ black and$ 30$ pieces of milk (not necessarily arranged in a checkerboard pattern). Can any such tile be broken into three rectangles so that either each rectangle has an even number of black pieces, or each rectangle has an even number of milk pieces?
On the midline of the isosceles trapezoid $ABCD$ ($BC \parallel AD$) find the point $K$, for which the sum of the angles $\angle DAK + \angle BCK$ will be the smallest.
Inside the parallelogram $ABCD$, choose a point $P$ such that $\angle APB+ \angle CPD= \angle BPC+ \angle APD$. Prove that there exists a circle tangent to each of the circles circumscribed around the triangles $APB$, $BPC$, $CPD$ and $APD$.
A rectangle of size $5x11$ was cut along the cell lines into two identical shapes, from which you can make a square, and a number of individual cells. What is the smallest number of individual cells that could be formed?
Let $AD$ and $AE$ be the altitude and median of triangle $ABC$, in with $\angle B = 2\angle C$. Prove that $AB = 2DE$.
Let $ABC$ be an acute-angled triangle in which $AB <AC$. On the side $BC$ mark a point $D$ such that $AD = AB$, and on the side $AB$ mark a point $E$ such that the segment $DE$ passes through the orthocenter of triangle $ABC$. Prove that the center of the circumcircle of triangle $ADE$ lies on the segment $AC$.
Is it possible to place on a plane $5$ circles of radius $12$ and $12$ circles of radius $5$ so that each small circle touches one small and two large circles?
Given a triangle $ABC$. Construct a point $D$ on the side $AB$ and point $E$ on the side $AC$ so that $BD = CE$ and $\angle ADC = \angle BEC$
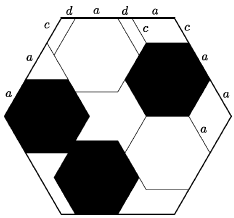
The symbol of the Olympiad shows $5$ regular hexagons with side $a$, located inside a regular hexagon with side $b$. Find ratio $\frac{a}{b}$.
A rectangle was cut into smaller rectangles by horizontal and vertical lines so that there was at least one horizontal and at least one vertical section. It turned out that the areas of all formed rectangles form an arithmetic progression. Prove that all these rectangles are equal.
Let $O$ be the center of the circle circumscribed around the acute triangle $ABC$, and let $N$ be the midpoint of the arc $ABC$ of this circle. On the sides $AB$ and $BC$ mark points $D$ and $E$ respectively, such that the point $O$ lies on the segment $DE$. The lines $DN$ and $BC$ intersect at the point $P$, and the lines $EN$ and $AB$ intersect at the point $Q$. Prove that $PQ \perp AC$.
A square and several straight lines that do not pass through its vertices are drawn on the plane. For each side and each diagonal of the square, calculate the number of lines that intersect this segment. Could it be that these numbers are six consecutive natural numbers?
Let $ABC$ be an acute triangle, $D$ be the midpoint of $BC$. Bisectors of angles $ADB$ and $ADC$ intersect the circles circumscribed around the triangles $ADB$ and $ADC$ at points $E$ and $F$, respectively. Prove that $EF\perp AD$.
The diagonals of the cyclic quadrilateral $ABCD$ intersect at the point $E$. Let $P$ and $Q$ are the centers of the circles circumscribed around the triangles $BCE$ and $DCE$, respectively. A straight line passing through the point $P$ parallel to $AB$, and a straight line passing through the point $Q$ parallel to $AD$, intersect at the point $R$. Prove that the point $R$ lies on segment $AC$.
Let $I$ be the center of a circle inscribed in triangle $ABC$, in which $\angle BAC = 60 ^o$ and $AB \ne AC$. The points $D$ and $E$ were marked on the rays $BA$ and $CA$ so that $BD = CE = BC$. Prove that the line $DE$ passes through the point $I$.
Let $D$ be a point on the side $AB$ of the triangle $ABC$ such that $BD = CD$, and let the points $E$ on the side $BC$ and $F$ on the extension $AC$ beyond the point $C$ be such that $EF\parallel CD$. The lines $AE$ and $CD$ intersect at the point $G$. Prove that $BC$ is the bisector of the angle $FBG$.
details of issues of magazine ''У світі математики'' that were posted the missing correspondece MOs:
2003 /9/4 VIII Всеукраїнська заочна математична олімпіада
2002 /8/4 VII Всеукраїнська заочна математична олімпіада
2001 /7/4 VI Всеукраїнська заочна математична олімпіада
2000 /6/4 V Всеукраїнська заочна математична олімпіада
1999 /?? IV Всеукраїнська заочна математична олімпіада
1998 /4/3 (III) Третя Всеукраїнська заочна олімпіада
1997 /3/4 (II) Заочна математична олімпіада журналу “У світі математики”
1996 /2/4 (I) Заочна математична олімпіада журналу “У світі математики”
No comments:
Post a Comment