drop down menu

Princeton University MC 2006-20 (PUMaC) 243p

geometry problems from Princeton University Mathematics Competition (PUMaC)
with aops links in the names


collected inside aops:
2006 - 2020 


$A,B,C,D,E$, and $F$ are points of a convex hexagon, and there is a circle such that $A,B,C,D,E$, and $F$ are all on the circle. If $\angle ABC = 72^o$, $\angle BCD = 96^o$, $\angle CDE = 118^o$, and $\angle DEF = 104^o$, what is $\angle EFA$?

$ABC$ is an equilateral triangle with side length $ 1$. $BCDE$ is a square. Some point $F$ is equidistant from $A, D$, and $E$. Find the length of $AF$.
Find the exact value of $\sin 36^o$.

There is a circle $c$ centered about the origin of radius $ 1$. There are circles $c_1$,$ . . .$ ,$c_6$, each of radius $r_1$, such that each circle is completely inside c and is tangent to it, and $c_2$ is tangent to $c_1$, $c_3$ is tangent to $c_2$, . . ., and $c_1$ is tangent to $c_6$. There is a circle $d$ which is tangent to $c$, $c_1$, and $c_2$, but does not intersect any of these circles. What is the radius of circle $d$? Express your answer in the form $\frac{a+b\sqrt{c}}{d}$ , where $a,b,c,d$ are integers, $d$ is positive and as small as possible, and $c$ is squarefree.

$A, B$, and $C$ are vertices of a triangle, and $P$ is a point within the triangle. If angles $\angle BAP$, $\angle BCP$, and $\angle ABP$ are all $30^o$ and angle $\angle ACP$ is $45^o$, what is $\sin(\angle CBP)$?

Given that in the diagram shown, $\angle ACB = 65^o$, $\angle BAC = 50^o$, $\angle BDC = 25^o$, $AB = 5$, and $AE = 1$, determine the value of $BE \cdot DE$.
Given parallelogram $ABCD$, construct point $F$ so that $CF\perp BC$, as shown. Also $F$ is placed so that $\angle DFC = 120^o$. If $DF = 4$ and $BC =CF = 2$, what is the area of the parallelogram?

Given that triangle $ABC$ has side lengths $a=7$, $b=8$ , $c=5$, find$$(\sin (A)+\sin (B)+\sin (C)) \cdot \left(\cot \frac{A}{2}+\cot \frac{B}{2}+\cot \frac{C}{2}\right).$$.

Consider all line segments of length $4$ with one end-point on the line $y = x$ and the other end-point on the line $y = 2x$. Find the equation of the locus of the midpoints of these line segments.
Points $P$ and $Q$ are located inside square $ABCD$ such that $DP$ is parallel to $QB$ and $DP = QB = PQ$. Determine the minimum possible value of $\angle ADP$.

In triangle $ABC$, $R$ is the midpoint of $BC$ and $CS = 3SA$. If $x$ is the area of $CRS$, $y$ is the area of $RBT$, $z$ is the area of $ATS$, and $y^2 = xz$, then what is the value of $\frac{AT}{TB}$?
Express your answer in the form $\frac{a+b\sqrt{c}}{d}$ , where $a,b,c,d$ are integers, $d$ is positive and as small as possible, and $c$ is squarefree.

Triangle $ABC$ has $AC = 3$, $BC = 5$, $AB = 7$. A circle is drawn internally tangent to the circumcircle of $ABC$ at $C$, and tangent to $AB$. Let $D$ be its point of tangency with $AB$. Find $BD - DA$.
$A, B, C$, and $D$ are all on a circle, and $ABCD$ is a convex quadrilateral. If $AB = 13$, $BC = 13$, $CD = 37$, and $AD = 47$, what is the area of $ABCD$?

Points $P_1, P_2, P_3,$ and $P_4$ are $(0,0), (10, 20), (5, 15),$ and $(12, -6)$, respectively. For what point $P \in \mathbb{R}^2$ is the sum of the distances from $P$ to the other $4$ points minimal?

Find $\frac{area(CDF)}{area(CEF)}$ in the figure.
$A$ and $B$ are on a circle of radius $20$ centered at $C$, and $\angle ACB = 60^\circ$. $D$ is chosen so that $D$ is also on the circle, $\angle ACD = 160^\circ$, and $\angle DCB = 100^\circ$. Let $E$ be the intersection of lines $AC$ and $BD$. What is $DE$

A sphere of radius $\sqrt{85}$ is centered at the origin in three dimensions. A tetrahedron with vertices at integer lattice points is inscribed inside the sphere. What is the maximum possible volume of this tetrahedron?

A set of points $P_i$ covers a polygon if for every point in the polygon, a line can be drawn inside the polygon to at least one $P_i$. Points $A_1, A_2, \cdots, A_n$ in the plane form a $2007$-gon, not necessarily convex. Find the minimum value of $n$ such that for any such polygon, we can pick $n$ points inside it that cover the polygon.

What is the area of the region defined by $x^2+3y^2 \le 4$ and $y^2+3x^2 \le 4$?

There are four spheres each of radius $1$ whose centers form a triangular pyramid where each side has length $2$. There is a 5th sphere which touches all four other spheres and has radius less than $1$. What is its radius?

In triangle $ABC$ with $AB \neq AC$, points $N \in CA$, $M \in AB$, $P \in BC$, and $Q \in BC$ are chosen such that $MP \parallel AC$, $NQ \parallel AB$, $\frac{BP}{AB} = \frac{CQ}{AC}$, and $A, M, Q, P, N$ are concyclic. Find $\angle BAC$.

A pirate ship spots, $10$ nautical miles to the east, an oblivious caravel sailing $60$ south of west at a steady $12 \text{ nm/hour}$. What is the minimum speed that the pirate ship must maintain at to be able to catch the caravel?

A black witch's hat is in the classic shape of a cone on top of a circular brim. The cone has a slant height of $18$ inches and a base radius of $3$ inches. The brim has a radius of $5$ inches. What is the total surface area of the hat?

Suppose that $ABCD$ is a rectangle with sides of length $12$ and $18$. Let $S$ be the region of points contained in $ABCD$ which are closer to the center of the rectangle than to any of its vertices. Find the area of $S$.

$ABCDE$ is a regular pentagon (with vertices in that order) inscribed in a circle of radius $1$. Find $AB \cdot AC$.

Four circles of radius $1$ are each tangent to two sides (line segments) of a square and externally tangent to a circle of radius $3$. What is the area of the space that is inside the square but not contained in any of the circles?

Let $C$ and $D$ be two points, not diametrically opposite, on a circle $C_1$ with center $M$. Let $H$ be a point on minor arc $CD$. The tangent to $C_1$ at $H$ intersects the circumcircle of $CMD$ at points $A$ and $B$. Prove that $CD$ bisects $MH$ iff $\angle AMB = \frac{\pi}{2}$

In triangle $ABC$, let $O$ and $I_A$ be the centers of the circumcircle and the circle tangent to $AB$ and $AC$ and externally tangent to $BC$, and let $R$ and $R_A$ be their radii. Find $ \frac {I_A A \cdot I_A B \cdot I_A C}{R \cdot R_A^2} $.

In triangle $ABC$, $Q$ and $R$ are points on segments $AC$ and $AB$, respectively, and $P$ is the intersection of $CR$ and $BQ$. If $AR=RB=CP$ and $CP=PQ$, find $ \angle BRC $.

What is the area of a circle with a circumference of $8$?

Consider a convex polygon $\mathcal{P}$ in space with perimeter $20$ and area $30$. What is the volume of the locus of points that are at most $1$ unit away from some point in the interior of $\mathcal{P}$?

Consider a $12$-sided regular polygon. If the vertices going clockwise are $A$, $B$, $C$, $D$, $E$, $F$, etc, draw a line between $A$ and $F$, $B$ and $G$, $C$ and $H$, etc. This will form a smaller $12$-sided regular polygon in the center of the larger one. What is the area of the smaller one divided by the area of the larger one?

How many ordered pairs of real numbers $(x, y)$ are there such that $x^2+y^2 = 200$ and
$\sqrt{(x-5)^2+(y-5)^2}+\sqrt{(x+5)^2+(y+5)^2}$ is an integer?

Infinitesimal Randall Munroe is glued to the center of a pentagon with side length $1$. At each corner of the pentagon is a confused infinitesimal velociraptor. At any time, each raptor is running at one unit per second directly towards the next raptor in the pentagon (in counterclockwise order). How far does each confused raptor travel before it reaches Randall Munroe?

Find the coordinates of the point in the plane at which the sum of the distances from it to the three points $(0, 0)$, $(2, 0)$, $(0, \sqrt{3})$ is minimal.

Let $\mathcal{H}$ be the region of points $(x, y)$, such that $(1, 0), (x, y), (-x, y)$, and $(-1,0)$ form an isosceles trapezoid whose legs are shorter than the base between $(x, y)$ and $(-x,y)$. Find the least possible positive slope that a line could have without intersecting $\mathcal{H}$.

In four-dimensional space, the $24$-cell of sidelength $\sqrt{2}$ is the convex hull of (smallest convex set containing) the $24$ points $(\pm 1, \pm 1, 0, 0)$ and its permutations. Find the four-dimensional volume of this region.

In tetrahedron $ABCD$ with circumradius $2$, $AB = 2$, $CD = \sqrt{7}$, and $\angle ABC = \angle BAD = \frac{\pi}{2}$. Find all possible angles between the planes containing $ABC$ and $ABD$.

A cuboctahedron is the convex hull of (smallest convex set containing) the $12$ points $(\pm 1, \pm 1, 0), (\pm 1, 0, \pm 1), (0, \pm 1, \pm 1)$. Find the cosine of the solid angle of one of the triangular faces, as viewed from the origin. (Take a figure and consider the set of points on the unit sphere centered on the origin such that the ray from the origin through the point intersects the fi gure. The area of that set is the solid angle of the fi gure as viewed from the origin.)

If a rectangle’s length is increased by $30\%$ and its width is decreased by $30\%$, by what percentage does its area change? State whether the area increases or decreases.

A cube is divided into $27$ unit cubes. A sphere is inscribed in each of the corner unit cubes, and another sphere is placed tangent to these $8$ spheres. What is the smallest possible value for the radius of the last sphere?

Two externally tangent circles have radius $2$ and radius $3$. Two lines are drawn, each tangent to both circles, but not at the point where the circles are tangent to each other. What is the area of the quadrilateral whose vertices are the four points of tangency between the circles and the lines?

Circles $A, B$, and $C$ each have radius $r$, and their centers are the vertices of an equilateral triangle of side length $6r$. Two lines are drawn, one tangent to $A$ and $C$ and one tangent to $B$ and $C$, such that $A$ is on the opposite side of each line from $B$ and $C$. Find the sine of the angle between the two lines.
Let $P$ be a convex polygon, and let $n \ge 3$ be a positive integer. On each side of $P$, erect a regular $n$-gon that shares that side of $P$, and is outside $P$. If none of the interiors of these regular n-gons overlap, we call P $n$-good.
(a) Find the largest value of $n$ such that every convex polygon is $n$-good.
(b) Find the smallest value of $n$ such that no convex polygon is $n$-good.

Quadrilateral $ABCD$ has both an inscribed and a circumscribed circle and sidelengths $BC = 4, CD = 5, DA = 6$. Find the area of $ABCD$.


A rectangular piece of paper $ABCD$ has sides of lengths $AB = 1$, $BC = 2$. The rectangle is folded in half such that $AD$ coincides with $BC$ and $EF$ is the folding line. Then fold the paper along a line $BM$ such that the corner $A$ falls on line $EF$. How large, in degrees, is $\angle ABM$?

Tetrahedron $ABCD$ has sides of lengths, in increasing order, $7, 13, 18, 27, 36, 41$. If $AB=41$, then what is the length of $CD$?

A polygon is called concave if it has at least one angle strictly greater than $180^{\circ}$. What is the maximum number of symmetries that an 11-sided concave polygon can have? (A symmetry of a polygon is a way to rotate or reflect the plane that leaves the polygon unchanged.)

In the following diagram (not to scale), $A$, $B$, $C$, $D$ are four consecutive vertices of an 18-sided regular polygon with center $O$. Let $P$ be the midpoint of $AC$ and $Q$ be the midpoint of $DO$. Find $\angle OPQ$ in degrees.
Lines $l$ and $m$ are perpendicular. Line $l$ partitions a convex polygon into two parts of equal area, and partitions the projection of the polygon onto $m$ into two line segments of length $a$ and $b$ respectively. Determine the maximum value of $\left\lfloor \frac{1000a}{b} \right\rfloor$. (The floor notation $\lfloor x \rfloor$ denotes largest integer not exceeding $x$

Consider the solid with 4 triangles and 4 regular hexagons as faces, where each triangle borders 3 hexagons, and all the sides are of length 1. Compute the [i]square[/i] of the volume of the solid. Express your result in reduced fraction and concatenate the numerator with the denominator (e.g., if you think that the square is $\frac{1734}{274}$, then you would submit 1734274).

You are given a convex pentagon $ABCDE$ with $AB=BC$, $CD=DE$, $\angle{ABC}=150^\circ$, $\angle{BCD} = 165^\circ$, $\angle{CDE}=30^\circ$, $BD=6$. Find the area of this pentagon. Round your answer to the nearest integer if necessary.
Consider $\triangle ABC$ and a point $M$ in its interior so that $\angle MAB = 10^\circ$, $\angle MBA = 20^\circ$, $\angle MCA = 30^\circ$ and $\angle MAC = 40^\circ$. What is $\angle MBC$?

2009 PUMaC Geometry B1
Find 100 times the area of a regular dodecagon inscribed in a unit circle. Round your answer to the nearest integer if necessary.
2009 PUMaC Geometry B2
A triangle has sides of lengths 5, 6, 7. What is 60 times the square of the radius of the inscribed circle?

A line drawn from vertex $A$ of equilateral $\triangle ABC $ meets $BC$ at $D$ and the circumcircle at $P$. If $BP = 55$ and $PC = 220$, find $AD$.

In right $\triangle ABC$, $P$ and $Q$ are on legs $BC$ and $AC$, respectively, such that $CP = CQ = 20$. Through the point of intersection, $R$, of $AP$ and $BQ$, a line is drawn also passing through $C$ and meeting the hypotenuse $AB$ at $S$. The extension of $PQ$ meets line $AB$ at $T$. Suppose $AB = 100$, and $AC = 80$. Then, if the length of $TS$ is $k$, find $k$.

The sidelengths of a triangle are $130$, $144$, and $194$. What is the area of its circumcircle?




2010 PUMaC Geometry A1/B3
As in the following diagram, square $ABCD$ and square $CEFG$ are placed side by side (i.e. $C$ is between $B$ and $E$ and $G$ is between $C$ and $D$). If $CE = 14$, $AB > 14$, compute the minimal area of $\triangle AEG$. 

2010 PUMaC Geometry A2/B5
In a rectangular plot of land, a man walks in a very peculiar fashion. Labeling the corners $ABCD$, he starts at $A$ and walks to $C$. Then, he walks to the midpoint of side $AD$, say $A_1$. Then, he walks to the midpoint of side $CD$ say $C_1$, and then the midpoint of $A_1D$ which is $A_2$. He continues in this fashion, indefinitely. The total length of his path if $AB=5$ and $BC=12$ is of the form $a + b\sqrt{c}$. Find $\displaystyle\frac{abc}{4}$.

Triangle $ABC$ has $AB = 4$, $AC = 5$, and $BC = 6$.  An angle bisector is drawn from angle $A$, and meets $BC$ at $M$.  What is the nearest integer to $100 \frac{AM}{CM}$?

In regular hexagon $ABCDEF$, $AC$, $CE$ are two diagonals. Points $M$, $N$ are on $AC$, $CE$ respectively and satisfy $AC: AM = CE: CN = r$. Suppose $B, M, N$ are collinear, find $100r^2$.

2010 PUMaC Geometry A5/B7
A cuboctahedron is a solid with 6 square faces and 8 equilateral triangle faces, with each edge adjacent to both a square and a triangle (see picture).  Suppose the ratio of the volume of an octahedron to a cuboctahedron with the same side length is $r$. Find $100r^2$.

In the following diagram, a semicircle is folded along a chord $AN$ and intersects its diameter $MN$ at $B$. Given that $MB : BN = 2 : 3$ and $MN = 10$. If $AN = x$, find $x^2$.
Square $ABCD$ is divided into four rectangles by $EF$ and $GH$. $EF$ is parallel to $AB$ and $GH$ parallel to $BC$.  $\angle BAF = 18^\circ$. $EF$ and $GH$ meet at point $P$. The area of rectangle $PFCH$ is twice that of rectangle $AGPE$. Given that the value of $\angle FAH$ in degrees is $x$, find the nearest integer to $x$.
2010 PUMaC Geometry A8
There is a point source of light in an empty universe. What is the minimum number of solid balls (of any size) one must place in space so that any light ray emanating from the light source intersects at least one ball?

In a polygon, every external angle is one sixth of its corresponding internal angle. How many sides does the polygon have?

On rectangular coordinates, point $A = (1,2)$, $B = (3,4)$. $P = (a, 0)$ is on $x$-axis. Given that $P$ is chosen such that $AP + PB$ is minimized, compute $60a$.

2010 PUMaC Geometry B4
Unit square $ABCD$ is divided into four rectangles by $EF$ and $GH$, with $BF = \frac14$. $EF$ is parallel to $AB$ and $GH$ parallel to $BC$. $EF$ and $GH$ meet at point $P$. Suppose $BF + DH = FH$, calculate the nearest integer to the degree of $\angle FAH$.
Point $P$ is in the interior of $\triangle ABC$. The side lengths of $ABC$ are $AB = 7$, $BC = 8$, $CA = 9$. The three foots of perpendicular lines from $P$ to sides $BC$, $CA$, $AB$ are $D$, $E$, $F$ respectively. Suppose the minimal value of $\frac{BC}{PD} + \frac{CA}{PE} + \frac{AB}{PF}$ can be written as $\frac{a}{b}\sqrt{c}$, where $\gcd(a,b) = 1$ and $c$ is square free, calculate $abc$.

Tetrahedron $ABCD$ has base $\triangle BCD$ which is an equilateral triangle with side length $2$. $AB = AC = 3$ and $AD = 4$. Let $M$ be the centroid of tetrahedron $ABCD$ and $N$ be the centroid of $\triangle BCD$. Write $\displaystyle\frac{AN}{AM} = \displaystyle\frac{p}q$, where $p$ and $q$ are relatively prime integers. You are to submit the concatenation of $p$ and $q$.

What is the maximum number of angles greater than $\pi$ that a $45$-gon can have?

Right triangle $\triangle ABC$ has integer side lengths, one side of length $29$, and maximal perimeter. What is the length of the hypotenuse of this triangle?



Two logs of length 10 are laying on the ground touching each other. Their radii are 3 and 1, and the smaller log is fastened to the ground. The bigger log rolls over the smaller log without slipping, and stops as soon as it touches the ground again. The volume of the set of points swept out by the larger log as it rolls over the smaller one can be expressed as $n \pi$, where $n$ is an integer. Find $n$.

A rectangular piece of paper has corners labeled $A, B, C$, and $D$, with $BC = 80$ and $CD = 120$. Let $M$ be the midpoint of side $AB$. The corner labeled $A$ is folded along line $MD$ and the corner labeled $B$ is folded along line $MC$ until the segments $AM$ and $MB$ coincide. Let $S$ denote the point in space where $A$ and $B$ meet. If $H$ is the foot of the perpendicular from $S$ to the original plane of the paper, find $HM$.

Let $PQ$ and $PR$ be tangents to a circle $\omega$ with diameter $AB$ so that $A, Q, R, B$ lie on $\omega$ in that order. Let $H$ be the projection of $P$ onto $AB$ and let $AR$ and $PH$ intersect at $S$. If $\angle QPH = 30^{\circ}$ and $\angle HPR = 20^\circ$, find $\angle ASQ$ in degrees.

Let $ABC$ be a triangle with $AB = 15, BC = 17$, $CA = 21$, and incenter $I$. If the circumcircle of triangle $IBC$ intersects side $AC$ again at $P$, find $CP$.

Let $\ell_1$ and $\ell_2$ be two parallel lines, a distance of 15 apart. Points $A$ and $B$ lie on $\ell_1$ while points $C$ and $D$ lie on $\ell_2$ such that $\angle BAC = 30^\circ$ and $\angle ABD = 60^\circ$. The minimum value of $AD + BC$ is $a\sqrt b$, where $a$ and $b$ are integers and $b$ is squarefree. Find $a + b$.
Let $\omega_1$ be a circle of radius 6, and let $\omega_2$ be a circle of radius 5 that passes through the center $O$ of $\omega_1$. Let $A$ and $B$ be the points of intersection of the two circles, and let $P$ be a point on major arc $AB$ of $\omega_2$. Let $M$ and $N$ be the second intersections of $PA$ and $PB$ with $\omega_1$, respectively. Let $S$ be the midpoint of $MN$. As $P$ ranges over major arc $AB$ of $\omega_2$, the minimum length of segment $SA$ is $a/b$, where $a$ and $b$ are positive integers and $\gcd(a, b) = 1$. Find $a+b$.

Let $ABC$ be a triangle with $AB = 2, BC = 5, AC = 4$. Let $M$ be the projection of $C$ onto the external angle bisector at vertex $B$. Similarly, let $N$ be the projection of $B$ onto the external angle bisector at vertex $C$. If the ratio of the area of quadrilateral $BCNM$ to the area of triangle $ABC$ is $a/b$, where $a$ and $b$ are positive integers and $\gcd(a, b) = 1$, find $a + b$.

Let $ABC$ be a triangle with $\angle BAC = 60^\circ, BA = 2$, and $CA = 3$. A point $M$ is located inside $ABC$ such that $MB = 1$ and $MC = 2$. A semicircle tangent to $MB$ and $MC$ has its center $O$ on $BC$. Let $P$ be the intersection of the angle bisector of $\angle BAC$ and the perpendicular bisector of $AC$. If the ratio $OP/MO$ is $a/b$, where $a$ and $b$ are positive integers and $\gcd(a, b) = 1$, find $a + b$.

Let triangle $ABC$ have $\angle A = 70^\circ, \angle B = 60^\circ$, and $\angle C = 50^\circ$. Extend altitude $BH$ past $H$ to point $D$ so that $BD = BC$. Find $\angle BDA$ in degrees.

Let $ABCD$ be a trapezoid with $AD$ parallel to $BC$, $AD = 2$, and $BC = 1$. Let $M$ be the midpoint of $AD$, and let $P$ be the intersection of $BD$ with $CM$. Extend $AP$ to meet segment $CD$ at point $Q$. If the ratio $CQ/QD = a/b$, where $a$ and $b$ are positive integers and $\text{gcd}(a, b) = 1$, find $a + b$.

Let $\omega$ be a circle of radius $6$ with center $O$. Let $AB$ be a chord of $\omega$ having length $5$. For any real constant $c$, consider the locus $\mathcal{L}(c) $ of all points $P$ such that $PA^2 - PB^2 = c$. Find the largest value of $c$ for which the intersection of $\mathcal{L}(c)$ and $\omega$ consists of just one point.

Four circles are situated in the plane so that each is tangent to the other three. If three of the radii are $5$, $5$, and $8$, the largest possible radius of the fourth circle is $a/b$, where $a$ and $b$ are positive integers and gcd$(a, b) = 1$. Find $a + b$.

Let $ABC$ be an equilateral triangle having sides of length 1, and let $P$ be a point in the interior of $\Delta ABC$ such that $\angle ABP = 15 ^\circ$. Find, with proof, the minimum possible value of $AP + BP + CP$. 

Comment: 
In fact this question is incorrect, unfortunately. A more reasonable problem: Prove that $AP + BP + CP \ge \sqrt{3}$.

A regular octahedron is a convex polyhedron composed of eight congruent faces, each of which is an equilateral triangle, four of them meet at each vertex. For instance, the following diagram depicts a regular octahedron: Let $T$ be a regular octahedron of edge length $28$. What is the total surface area of $T$ , rounded to the nearest integer?




Three circles, with radii of $1, 1$, and $2$, are externally tangent to each other. The minimum possible area of a quadrilateral that contains and is tangent to all three circles can be written as $a + b\sqrt{c}$ where $c$ is not divisible by any perfect square larger than $1$. Find $a + b + c$

Two circles centered at $O$ and $P$ have radii of length $5$ and $6$ respectively. Circle $O$ passes through point $P$. Let the intersection points of circles $O$ and $P$ be $M$ and $N$. The area of triangle $\vartriangle MNP$ can be written in simplest form as $a/b$. Find $a + b$.

Six ants are placed on the vertices of a regular hexagon with an area of $12$. At each point in time, each ant looks at the next ant in the hexagon (in counterclockwise order), and measures the distance, $s$, to the next ant. Each ant then proceeds towards the next ant at a speed of $\frac{s}{100}$ units per year. After T years, the ants’ new positions are the vertices of a new hexagon with an area of $4$. T is of the form $a \ln b$, where $b$ is square-free. Find $a + b$.

A square is inscribed in an ellipse such that two sides of the square respectively pass through the two foci of the ellipse. The square has a side length of $4$. The square of the length of the minor axis of the ellipse can be written in the form $a + b\sqrt{c}$ where $a, b$, and $c$ are integers, and $c$ is not divisible by the square of any prime. Find the sum $a + b + c$.

Let $\vartriangle ABC$ be a triangle with $\angle BAC = 45^o, \angle BCA = 30^o$, and $AB = 1$. Point $D$ lies on segment $AC$ such that $AB = BD$. Find the square of the length of the common external tangent to the circumcircles of triangles $\vartriangle BDC$ and $\vartriangle ABC$.

Consider a pool table with the shape of an equilateral triangle. A ball of negligible size is initially placed at the center of the table. After it has been hit, it will keep moving in the direction it was hit towards and bounce off any edges with perfect symmetry. If it eventually reaches the midpoint of any edge, we mark the midpoint of the entire route that the ball has travelled through. Repeating this experiment, how many points can we mark at most?
An octahedron (a solid with 8 triangular faces) has a volume of $1040$. Two of the spatial diagonals intersect, and their plane of intersection contains four edges that form a cyclic quadrilateral. The third spatial diagonal is perpendicularly bisected by this plane and intersects the plane at the circumcenter of the cyclic quadrilateral. Given that the side lengths of the cyclic quadrilateral are $7, 15, 24, 20$, in counterclockwise order, the sum of the edge lengths of the entire octahedron can be written in simplest form as $a/b$. Find $a + b$.

Cyclic quadrilateral $ABCD$ has side lengths $AB = 2, BC = 3, CD = 5, AD = 4$. Find $\sin A \sin B(\cot A/2 + \cot B/2 + \cot C/2 + \cot D/2)^2$. Your answer can be written in simplest form as $a/b$. Find $a + b$.

During chemistry labs, we oftentimes fold a disk-shaped filter paper twice, and then open up a flap of the quartercircle to form a cone shape, as in the diagram. What is the angle $\theta$, in degrees, of the bottom of the cone when we look at it from the side?
A $6$-inch-wide rectangle is rotated $90$ degrees about one of its corners, sweeping out an area of $45\pi$ square inches, excluding the area enclosed by the rectangle in its starting position. Find the rectangle’s length in inches.

Let A be a regular $12$-sided polygon. A new $12$-gon B is constructed by connecting the midpoints of the sides of A. The ratio of the area of B to the area of A can be written in simplest form as $(a +\sqrt{b})/c$, where $a, b, c$ are integers. Find $a + b + c$.

Assume the earth is a perfect sphere with a circumference of $60$ units. A great circle is a circle on a sphere whose center is also the center of the sphere. There are three train tracks on three great circles of the earth. One is along the equator and the other two pass through the poles, intersecting at a $90$ degree angle. If each track has a train of length $L$ traveling at the same speed, what is the maximum value of $L$ such that the trains can travel without crashing?

A cyclic quadrilateral $ABCD$ has side lengths $AB = 3, BC = AD = 5$, and $CD = 8$. The radius of its circumcircle can be written in the form $a\sqrt{b}/c$, where $a, b, c$ are positive integers, $a, c$ are relatively prime, and $b$ is not divisible by the square of any prime. Find $a + b + c$.

Let $ABC$ be a triangle with incenter $I$, and let $D$ be the foot of the angle bisector from $A$ to $BC$.  Let $\Gamma$ be the circumcircle of triangle $BIC$, and let $PQ$ be a chord of $\Gamma$ passing through $D$.  Prove that $AD$ bisects $\angle PAQ$.

$ABCDE$ is a pentagon with $AB = BC = CD =\sqrt2$, $\angle ABC = \angle BCD = 120^o$ , and $\angle BAE = \angle CDE = 105^o$ . Find the area of triangle $\vartriangle BDE$. Your answer in its simplest form can be written as $\frac{a+\sqrt{b}}{c}$, where where $a, b, c$ are integers and $b$ is square-free. Find $abc$.

Find the area of the set of all points in the plane such that there exists a square centered around the point and having the following properties:
$\bullet$ The square has side length $7\sqrt2$.
$\bullet$ The boundary of the square intersects the graph of $xy = 0$ at at least $3$ points.

Three cones have bases on the same plane, externally tangent to each other. The cones all face the same direction. Two of the cones have radii of $2$, and the other cone has a radius of $3$. The two cones with radii $2$ have height $4$, and the other cone has height $6$. Let $V$ be the volume of the tetrahedron with three of its vertices as the three vertices of the cones and the fourth vertex as the center of the base of the cone with height $6$. Find $V^2$.




Let $O$ be a point with three other points $A,B,C$ and $\angle AOB=\angle BOC=\angle AOC=2\pi/3$. Consider the average area of the set of triangles $ABC$ where $OA,OB,OC\in\{3,4,5\}$. The average area can be written in the form $m\sqrt n$ where $m,n$ are integers and $n$ is not divisible by a perfect square greater than $1$. Find $m+n$.

An equilateral triangle is given. A point lies on the incircle of this triangle. If the smallest two distances from the point to the sides of the triangle is $1$ and $4$, the sidelength of this equilateral triangle can be expressed as $\tfrac{a\sqrt b}c$ where $(a,c)=1$ and $b$ is not divisible by the square of an integer greater than $1$. Find $a+b+c$.

Consider the shape formed from taking equilateral triangle $ABC$ with side length $6$ and tracing out the arc $BC$ with center $A$. Set the shape down on line $l$ so that segment $AB$ is perpendicular to $l$, and $B$ touches $l$. Beginning from arc $BC$ touching $l$, we roll $ABC$ along $l$ until both points $A$ and $C$ are on the line. The area traced out by the roll can be written in the form $n\pi$, where $n$ is an integer. Find $n$.

Draw an equilateral triangle with center $O$. Rotate the equilateral triangle $30^\circ, 60^\circ, 90^\circ$ with respect to $O$ so there would be four congruent equilateral triangles on each other. Look at the diagram. If the smallest triangle has area $1$, the area of the original equilateral triangle could be expressed as $p+q\sqrt r$ where $p,q,r$ are positive integers and $r$ is not divisible by a square greater than $1$. Find $p+q+r$.

Suppose you have a sphere tangent to the $xy$-plane with its center having positive $z$-coordinate. If it is projected from a point $P=(0,b,a)$ to the $xy$-plane, it gives the conic section $y=x^2$. If we write $a=\tfrac pq$ where $p,q$ are integers, find $p+q$.

On a circle, points $A,B,C,D$ lie counterclockwise in this order. Let the orthocenters of $ABC,BCD,CDA,DAB$ be $H,I,J,K$ respectively. Let $HI=2$, $IJ=3$, $JK=4$, $KH=5$. Find the value of $13(BD)^2$.

Given triangle $ABC$ and a point $P$ inside it, $\angle BAP=18^\circ$, $\angle CAP=30^\circ$, $\angle ACP=48^\circ$, and $AP=BC$. If $\angle BCP=x^\circ$, find $x$.

Three chords of a sphere, each having length $5,6,7$, intersect at a single point inside the sphere and are pairwise perpendicular. For $R$ the maximum possible radius of this sphere, find $R^2$.

We construct three circles: $O$ with diameter $AB$ and area $12+2x$, $P$ with diameter $AC$ and area $24+x$, and $Q$ with diameter $BC$ and area $108-x$. Given that $C$ is on circle $O$, compute $x$.

Triangle $ABC$ satisfies $\angle ABC=\angle ACB=78^\circ$. Points $D$ and $E$ lie on $AB,AC$ and satisfy $\angle BCD=24^\circ$ and $\angle CBE=51^\circ$. If $\angle BED=x^\circ$, find $x$.

Consider all planes through the center of a $2\times2\times2$ cube that create cross sections that are regular polygons. The sum of the cross sections for each of these planes can be written in the form $a\sqrt b+c$, where $b$ is a square-free positive integer. Find $a+b+c$

Circle $w$ with center $O$ meets circle $\Gamma$ at $X,Y,$ and $O$ is on $\Gamma$. Point $Z\in\Gamma$ lies outside $w$ such that $XZ=11$, $OZ=15$, and $YZ=13$. If the radius of circle $w$ is $r$, find $r^2$.

A tetrahedron $ABCD$ satisfies $AB=6$, $CD=8$, and $BC=DA=5$. Let $V$ be the maximum value of $ABCD$ possible. If we can write $V^4=2^n3^m$ for some integers $m$ and $n$, find $mn$.

Triangle $A_1B_1C_1$ is an equilateral triangle with sidelength $1$. For each $n>1$, we construct triangle $A_nB_nC_n$ from $A_{n-1}B_{n-1}C_{n-1}$ according to the following rule: $A_n,B_n,C_n$ are points on segments $A_{n-1}B_{n-1},B_{n-1}C_{n-1},C_{n-1}A_{n-1}$ respectively, and satisfy the following:\[\dfrac{A_{n-1}A_n}{A_nB_{n-1}}=\dfrac{B_{n-1}B_n}{B_nC_{n-1}}=\dfrac{C_{n-1}C_n}{C_nA_{n-1}}=\dfrac1{n-1}\]So for example, $A_2B_2C_2$ is formed by taking the midpoints of the sides of $A_1B_1C_1$. Now, we can write $\tfrac{|A_5B_5C_5|}{|A_1B_1C_1|}=\tfrac mn$ where $m$ and $n$ are relatively prime integers. Find $m+n$. (For a triangle $\triangle ABC$, $|ABC|$ denotes its area.)

Let $\gamma$ be the incircle of $\triangle ABC$ (i.e. the circle inscribed in $\triangle ABC$) and $I$ be the center of $\gamma$. Let $D$, $E$ and $F$ be the feet of the perpendiculars from $I$ to $BC$, $CA$, and $AB$ respectively. Let $D'$ be the point on $\gamma$ such that $DD'$ is a diameter of $\gamma$. Suppose the tangent to $\gamma$ through $D$ intersects the line $EF$ at $P$. Suppose the tangent to $\gamma$ through $D'$ intersects the line $EF$ at $Q$. Prove that $\angle PIQ + \angle DAD' = 180^{\circ}$.

The area of a circle centered at the origin, which is inscribed in the parabola $y=x^2-25$, can be expressed as $\tfrac ab\pi$, where $a$ and $b$ are coprime positive integers. What is the value of $a+b$?

 2013 PUMaC Team 11 
If two points are selected at random on a fixed circle and the chord between the two points is drawn, what is the probability that its length exceeds the radius of the circle?

2013 PUMaC Team 12 
Let $D$ be a point on the side $BC$ of $\triangle ABC$. If $AB=8$, $AC=7$, $BD=2$, and $CD=1$, find $AD$.



Let $x=\frac pq$ for $p$, $q$ coprime. Find $p+q$.
Triangle $ABC$ has lengths $AB=20$, $AC=14$, $BC=22$. The median from $B$ intersects $AC$ at $M$ and the angle bisector from $C$ intersects $AB$ at $N$ and the median from $B$ at $P$. Let $\dfrac pq=\dfrac{[AMPN]}{[ABC]}$ for positive integers $p$, $q$ coprime. Note that $[ABC]$ denotes the area of triangle $ABC$. Find $p+q$.

Let $O$ be the circumcenter of triangle $ABC$ with circumradius $15$. Let $G$ be the centroid of $ABC$ and let $M$ be the midpoint of $BC$. If $BC=18$ and $\angle MOA=150^\circ$, find the area of $OMG$.

Consider the cyclic quadrilateral with side lengths $1$, $4$, $8$, $7$ in that order. What is its circumdiameter? Let the answer be of the form $a\sqrt b+c$, for $b$ squarefree. Find $a+b+c$.

There is a point $D$ on side $AC$ of acute triangle $\triangle ABC$. Let $AM$ be the median drawn from $A$ (so $M$ is on $BC$) and $CH$ be the altitude drawn from $C$ (so $H$ is on $AB$). Let $I$ be the intersection of $AM$ and $CH$, and let $K$ be the intersection of $AM$ and line segment $BD$. We know that $AK=8$, $BK=8$, and $MK=6$. Find the length of $AI$.

$\triangle ABC$ has side lengths $AB=15$, $BC=34$, and $CA=35$. Let the circumcenter of $ABC$ be $O$. Let $D$ be the foot of the perpendicular from $C$ to $AB$. Let $R$ be the foot of the perpendicular from $D$ to $AC$, and let $W$ be the perpendicular foot from $D$ to $BC$. Find the area of quadrilateral $CROW$.

Let $O$ be the center of a circle of radius $26$, and let $A$, $B$ be two distinct points on the circle, with $M$ being the midpoint of $AB$. Consider point $C$ for which $CO=34$ and $\angle COM=15^\circ$. Let $N$ be the midpoint of $CO$. Suppose that $\angle ACB=90^\circ$. Find $MN$.

$ABCD$ is a cyclic quadrilateral with circumcenter $O$ and circumradius $7$. $AB$ intersects $CD$ at $E$, $DA$ intersects $CB$ at $F$. $OE=13$, $OF=14$. Let $\cos\angle FOE=\dfrac pq$, with $p$, $q$ coprime. Find $p+q$.

Consider the pyramid $OABC$. Let the equilateral triangle $ABC$ with side length $6$ be the base. Also $9=OA=OB=OC$. Let $M$ be the midpoint of $AB$. Find the square of the distance from $M$ to $OC$.

In $\triangle ABC$, $E\in AC$, $D\in AB$, $P=BE\cap CD$. Given that $S\triangle BPC=12$, while the areas of $\triangle BPD$, $\triangle CPE$ and quadrilateral $AEPD$ are all the same, which is $x$. Find the value of $x$.

Consider quadrilateral $ABCD$. It is given that $\angle DAC=70^\circ$, $\angle BAC=40^\circ$, $\angle BDC=20^\circ$, $\angle CBD=35^\circ$. Let $P$ be the intersection of $AC$ and $BD$. Find $\angle BPC$.

Let $\gamma$ be the incircle of $\triangle ABC$ (i.e. the circle inscribed in $\triangle ABC$) for which $AB+AC=3BC$. Let the point where $AC$ is tangent to $\gamma$ be $D$. Let the incenter of $I$. Let the intersection of the circumcircle of $\triangle BCI$ with $\gamma$ that is closer to $B$ be $P$. Show that $PID$ is collinear.

 2014 PUMaC Individual Finals B1
Let $A, B$ be two points on circle $\gamma$. At point $A$ and $B$ we construct tangents to $\gamma$, $AC$ and $BD$ respectively such that the tangents are both in the clockwise direction. Let the intersection between $AB$ and $CD$ be $P$ . If $AC = BD$, prove that $P$ bisects the line $CD$.

2014 PUMaC Team 2
Given a Pacman of radius $1$, and mouth opening angle $90^\circ$, what is the largest (circular) pellet it can eat? The pellet must lie entirely outside the yellow portion and entirely inside the circumcircle of the Pacman. Let the radius be equal to $a\sqrt b+c$. where $b$ is square free. Find $a+b+c$.

2014 PUMaC Team 4
$ABC$ is a right triangle with $AC=3$, $BC=4$, $AB=5$. Squares are erected externally on the sides of the triangle. Evaluate the area of hexagon $PQRSTU$.

2014 PUMaC Team 11
$\triangle ABC$ has $AB=4$ and $AC=6$. Let point $D$ be on line $AB$ so that $A$ is between $B$ and $D$. Let the angle bisector of $\angle BAC$ intersect line $BC$ at $E$, and let the angle bisector of $\angle DAC$ intersect line $BC$ at $F$. Given that $AE=AF$, find the square of the circumcircle's radius' length.

2014 PUMaC Team 13
There is a right triangle $\triangle ABC$ in which $\angle A$ is the right angle. On side $AB$, there are three points $X$, $Y$, and $Z$ that satisfy $\angle ACX=\angle XCY=\angle YCZ=\angle ZCB$ and $BZ=2AX$. The smallest angle of $\triangle ABC$ is $\tfrac ab$ degrees, where $a,b$ are positive integers such that $\gcd(a,b)=1$. Find $a+b$.


For her daughter’s $12\text{th}$ birthday, Ingrid decides to bake a dodecagon pie in celebration. Unfortunately, the store does not sell dodecagon shaped pie pans, so Ingrid bakes a circular pie first and then trims off the sides in a way such that she gets the largest regular dodecagon possible. If the original pie was $8$ inches in diameter, the area of pie that she has to trim off can be represented in square inches as $a\pi - b$ where $a, b$ are integers. What is $a + b$?

Terry the Tiger lives on a cube-shaped world with edge length $2$. Thus he walks on the outer surface. He is tied, with a leash of length $2$, to a post located at the center of one of the faces of the cube. The surface area of the region that Terry can roam on the cube can be represented as $\frac{p \pi}{q} + a\sqrt{b}+c$ for integers $a, b, c, p, q$ where no integer square greater than $1$ divides $b, p$ and $q$ are coprime, and $q > 0$. What is $p + q + a + b + c$? (Terry can be at a location if the shortest distance along the surface of the cube between that point and the post is less than or equal to $2$.)

Cyclic quadrilateral $ABCD$ satisfies $\angle ADC = 2 \cdot \angle BAD = 80^\circ$ and $\overline{BC} = \overline{CD}$. Let the angle bisector of $\angle BCD$ meet $AD$ at $P$. What is the measure, in degrees, of $\angle BP D$?

Find the largest $r$ such that $4$ balls each of radius $r$ can be packed into a regular tetrahedron with side length $1$. In a packing, each ball lies outside every other ball, and every ball lies inside the boundaries of the tetrahedron. If $r$ can be expressed in the form $\frac{\sqrt{a}+b}{c}$ where $a, b, c$ are integers such that $\gcd(b, c) = 1$, what is $a + b + c$?

Let $P, A, B, C$ be points on circle $O$ such that $C$ does not lie on arc $\widehat{BAP}$, $\overline{P A} = 21, \overline{P B} = 56, \overline{P C} = 35$ and $m \angle BP C = 60^\circ$. Now choose point $D$ on the circle such that $C$ does not lie on arc $\widehat{BDP}$ and $\overline{BD} = 39$. What is $AD$?

Triangle $ABC$ is inscribed in a unit circle $\omega$. Let $H$ be its orthocenter and $D$ be the foot of the perpendicular from $A$ to $BC$. Let $\triangle XY Z$ be the triangle formed by drawing the tangents to $\omega$ at $A, B, C$. If $\overline{AH} = \overline{HD}$ and the side lengths of $\triangle XY Z$ form an arithmetic sequence, the area of $\triangle ABC$ can be expressed in the form $\tfrac{p}{q}$ for relatively prime positive integers $p, q$. What is $p + q$?

Triangle $ABC$ has $\overline{AB} = \overline{AC} = 20$ and $\overline{BC} = 15$. Let $D$ be the point in $\triangle ABC$ such that $\triangle ADB \sim \triangle BDC$. Let $l$ be a line through $A$ and let $BD$ and $CD$ intersect $l$ at $P$ and $Q$, respectively. Let the circumcircles of $\triangle BDQ$ and $\triangle CDP$ intersect at $X$. The area of the locus of $X$ as $l$ varies can be expressed in the form $\tfrac{p}{q}\pi$ for positive coprime integers $p$ and $q$. What is $p + q$?

The incircle of acute triangle $ABC$ touches $BC, AC$, and $AB$ at points $D, E$, and $F$, respectively. Let $P$ be the second intersection of line $AD$ and the incircle. The line through $P$ tangent to the incircle intersects $AB$ and $AC$ at points $M$ and $N$, respectively. Given that $\overline{AB} = 8, \overline{AC} = 10$, and $\overline{AN} = 4$, let $\overline{AM} = \tfrac{a}{b}$ where $a$ and $b$ are positive coprime integers. What is $a + b$?

Find the distance $\overline{CF}$ in the diagram below where $ABDE$ is a square and angles and lengths are as given:
The length $\overline{CF}$ is of the form $a\sqrt{b}$ for integers $a, b$ such that no integer square greater than $1$ divides $b$. What is $a + b$?

Let $ABCD$ be a regular tetrahedron with side length $1$. Let $EF GH$ be another regular tetrahedron such that the volume of $EF GH$ is $\tfrac{1}{8}\text{-th}$ the volume of $ABCD$. The height of $EF GH$ (the minimum distance from any of the vertices to its opposing face) can be written as $\sqrt{\tfrac{a}{b}}$, where $a$ and $b$ are positive coprime integers. What is $a + b$?

Let $I$ be the incenter of a triangle $ABC$ with $AB = 20$, $BC = 15$, and $BI = 12$. Let $CI$ intersect the circumcircle $\omega_1$ of $ABC$ at $D \neq C $. Alice draws a line $l$ through $D$ that intersects $\omega_1$ on the minor arc $AC$ at $X$ and the circumcircle $\omega_2$ of $AIC$ at $Y$ outside $\omega_1$. She notices that she can construct a right triangle with side lengths $ID$, $DX$, and $XY$. Determine, with proof, the length of $IY$.

On a circle $\omega_1$, four points $A$, $C$, $B$, $D$ lie in that order. Prove that $CD^2 = AC \cdot BC + AD \cdot BD$ if and only if at least one of $C$ and $D$ is the midpoint of arc $AB$.

Imagine a regular a $2015$-gon with edge length $2$. At each vertex, draw a unit circle centered at that vertex and color the circle’s circumference orange. Now, another unit circle $S$ is placed inside the polygon such that it is externally tangent to two adjacent circles centered at the vertices. This circle $S$ is allowed to roll freely in the interior of the polygon as long as it remains externally tangent to the vertex circles. As it rolls, $S$ turns the color of any point it touches into black. After it rolls completely around the interior of the polygon, the total length of the black lengths can be expressed in the form $\tfrac{p\pi}{q}$ for positive integers $p, q$ satisfying $\gcd(p, q) = 1$. What is $p + q$?

Charlie noticed his golden ticket was golden in two ways! In addition to being gold, it was a rectangle whose side lengths had ratio the golden ratio $\varphi = \tfrac{1+\sqrt{5}}{2}$. He then folds the ticket so that two opposite corners (vertices connected by a diagonal) coincide and makes a sharp crease (the ticket folds just as any regular piece of paper would). The area of the resulting shape can be expressed as $a + b \varphi$. What is $\tfrac{b}{a}$?

Triangle $ABC$ has $\overline{AB} = 5, \overline{BC} = 4, \overline{CA} = 6$. Points $D$ and $E$ are on sides $AB$ and $AC$, respectively, such that $\overline{AD} = \overline{AE} = \overline{BC}$. Let $CD$ and $BE$ intersect at $F$ and let $AF$ and $DE$ intersect at $G$. The length of $FG$ can be expressed in the form $\tfrac{a\sqrt{b}}{c}$ in simplified form. What is $a + b + c$?

Alice is stacking balls on the ground in three layers using two sizes of balls: small and large. All small balls are the same size, as are all large balls. For the first layer, she uses $6$ identical large balls $A, B, C, D, E$, and $F$ all touching the ground and so that $D, E, F$ touch each other, A touches $E$ and $F$, $B$ touches $D$ and $F$, and $C$ touches $D$ and $E$. For the second layer, she uses $3$ identical small balls, $G, H$, and $I$; $G$ touches $A, E$, and $F, H$ touches $B, D$, and $F$, and $I$ touches $C, D$, and $E$. Obviously, the small balls do not intersect the ground. Finally, for the top layer, she uses one large ball that touches $D, E, F, G, H$, and $I$. If the large balls have volume $2015$, the sum of the volumes of all the balls in the pyramid can be written in the form $a\sqrt{b}+c$ for integers $a, b, c$ where no integer square larger than $1$ divides $b$. What is $a + b + c$? (This diagram may not have the correct scaling, but just serves to clarify the layout of the problem.)




Let $\vartriangle ABC$ be an equilateral triangle with side length $1$ and let $\Gamma$ the circle tangent to $AB$ and $AC$ at $B$ and $C$, respectively. Let $P$ be on side $AB$ and $Q$ be on side $AC$ so that $PQ // BC$, and the circle through $A, P$, and $Q$ is tangent to $\Gamma$ . If the area of $\vartriangle APQ$ can be written in the form $\frac{\sqrt{a}}{b}$ for positive integers $a$ and $b$, where $a$ is not divisible by the square of any prime, find $a + b$.

2016 PUMaC Geometry A2 / B3
Let $ABCD$ be a square with side length $8$. Let $M$ be the midpoint of $BC$ and let $\omega$ be the circle passing through $M, A$, and $D$. Let $O$ be the center of $\omega, X$ be the intersection point (besides A) of $\omega$ with $AB$, and $Y$ be the intersection point of $OX$ and $AM$. If the length of $OY$ can be written in simplest form as $\frac{m}{n}$ , compute $m + n$.

Let $C$ be a right circular cone with apex $A$. Let $P_1, P_2, P_3, P_4$ and $P_5$ be points placed evenly along the circular base in that order, so that $P_1P_2P_3P_4P_5$ is a regular pentagon. Suppose that the shortest path from $P_1$ to $P_3$ along the curved surface of the cone passes through the midpoint of $AP_2$. Let $h$ be the height of $C$, and $r$ be the radius of the circular base of $C$. If $\left(\frac{h}{r}\right)^2$ can be written in simplest form as $\frac{a}{b}$ , find $a + b$.

Let $\vartriangle ABC$ be a triangle with integer side lengths such that $BC = 2016$. Let $G$ be the centroid of $\vartriangle ABC$ and $I$ be the incenter of $\vartriangle ABC$. If the area of $\vartriangle BGC$ equals the area of $\vartriangle BIC$, find the largest possible length of $AB$.

Let $D, E$, and $F$ respectively be the feet of the altitudes from $A, B$, and $C$ of acute triangle $\vartriangle ABC$ such that $AF = 28, FB = 35$ and $BD = 45$. Let $P$ be the point on segment $BE$ such that $AP = 42$. Find the length of $CP$.

In isosceles triangle $ABC$ with base $BC$, let $M$ be the midpoint of $BC$. Let $P$ be the intersection of the circumcircle of $\vartriangle ACM$ with the circle with center $B$ passing through $M$, such that $P \ne M$. If $\angle BPC = 135^o$, then $\frac{CP}{AP}$ can be written as $a +\sqrt{b}$ for positive integers $a$ and $b$, where $b$ is not divisible by the square of any prime. Find $a + b$.

Let $ABCD$ be a cyclic quadrilateral with circumcircle $\omega$ and let $AC$ and $BD$ intersect at $X$. Let the line through $A$ parallel to $BD$ intersect line $CD$ at $E$ and $\omega$ at $Y \ne A$. If $AB = 10, AD = 24, XA = 17$, and $XB = 21$, then the area of $\vartriangle DEY$ can be written in simplest form as $\frac{m}{n}$ . Find $m + n$.

Let $\vartriangle ABC$ have side lengths $AB = 4,BC = 6,CA = 5$. Let $M$ be the midpoint of $BC$ and let $P$ be the point on the circumcircle of $\vartriangle ABC$ such that $\angle MPA = 90^o$. Let $D$ be the foot of the altitude from $B$ to $AC$, and let $E$ be the foot of the altitude from $C$ to $AB$. Let $PD$ and $PE$ intersect line $BC$ at $X$ and $Y$ , respectively. Compute the square of the area of $\vartriangle AXY$ .

A circle of radius 1 has four circles $\omega_1, \omega_2, \omega_3$, and $\omega_4$ of equal radius internally tangent to it, so that $\omega_1$ is tangent to $\omega_2$, which is tangent to $\omega_3$, which is tangent to $\omega_4$, which is tangent to $\omega_1$, as shown. The radius of the circle externally tangent to $\omega_1, \omega_2, \omega_3$, and $\omega_4$ has radius r. If $r = a -\sqrt{b}$ for positive integers $a$ and $b$, compute $a + b$.
Let $V$ be the volume of the octahedron $ABCDEF$ with $A$ and $F$ opposite, $B$ and $E$ opposite, and $C$ and $D$ opposite, such that $AB = AE = EF = BF = 13$, $BC = DE = BD = CE = 14$, and $CF = CA = AD = FD = 15$. If $V = a\sqrt{b}$ for positive integers $a$ and $b$, where $b$ is not divisible by the square of any prime, find $a + b$.

On a cyclic quadrilateral $ABCD$, $M$ is the midpoint of $AB$ and $N$ is the midpoint of $CD$. Let $E$ be the projection of $C$ onto $AB$ and $F$ the reflection of $N$ about the midpoint of $DE$. If $F$ is inside quadrilateral $ABCD$, show that $\angle BMF = \angle CBD$.

Quadrilateral $ABCD$ has integer side lengths, and angles $ABC, ACD$, and $BAD$ are right angles. Compute the smallest possible value of $AD$.

Temerant is a spherical planet with radius $1000$ kilometers. The government wants to build twelve towers of the same height on the equator of Temerant, so that every point on the equator can be seen from at least one tower. The minimum possible height of the towers can be written, in kilometers, as a $\sqrt{b} - c\sqrt{d} - e$ for positive integers $a, b, c, d$, and $e$ (with $b$ and $d$ not divisible by the square of any prime). Compute $a + b + c + d + e$.

In triangle $ABC$, let $S$ be on $BC$ and $T$ be on $AC$ so that $AS  \perp BC$ and $BT \perp AC$, and let $AS$ and $BT$ intersect at $H$. Let $O$ be the center of the circumcircle of $\vartriangle AHT, P$ be the center of the circumcircle of $\vartriangle BHS$, and $G$ be the other point of intersection (besides $H$) of the two circles. Let $GH$ and $OP$ intersect at $X$. If $AB = 14, BH = 6$, and HA = 11, then $XO - XP$ can be written in simplest form as $\frac{m}{n}$ . Find $m + n$.

Let $\vartriangle ABC$ be a right triangle with $AB = 4, BC = 5$, and hypotenuse $AC$. Let I be the incenter of $\vartriangle ABC$ and $E$ be the excenter of $\vartriangle ABC$ opposite $A$ (the center of the circle tangent to $BC$ and the extensions of segments $AB$ and $AC$). Suppose the circle with diameter $IE$ intersects line $AB$ beyond $B$ at $D$. If $BD =\sqrt{a}- b$, where a and b are positive integers. Find $a + b$.

Let $ABCD$ be a rectangle of side lengths $3$ and $4$. Imagine folding the rectangle over the diagonal $BD$. The area of the new shape can be written with integers $a, b$ in the form $\frac{a}{b}$, where $\gcd (a, b) = 1$. What is $a + b$? (If there is overlapping area, it should only be considered once.)

Heesu draws an equilateral triangle $ABC$ with side $ 1$ m on a large piece of paper, then throws a dart at it. The dart lies within $1$ m of two of $A, B$, or $C$ (it could be inside or outside the triangle). The probability that it lies within $1$ m of all three vertices given it lies within $ 1$ m of two can be expressed in the form $\frac{a}{a+\pi}$ where $a = b\pi - c\sqrt{d}$. What is $b + c + d$?

A flashlight with angle measure $\theta$ is a device that can be positioned at any point $P$ on the coordinate plane and it illuminates everything in some angle of measure $\theta$ from vertex $P$. Flashlights of angle measure $60^o$ are positioned at $(0, 0)$ and $(0, 2)$ so that they shine directly at each other. Let $R$ be the region of the plane where a flashlight of angle measure $135^o$ could be positioned so that every flashlight is illuminated by every other flashlight. The area of R can be written in reduced form as $\frac{a\sqrt{b}-c \pi}{d}$. Compute $a + b + c + d$

How many tetrahedra have side lengths of $2,3,4,5,6,7$?

Triangle $ABC$ has circumradius $201$ and inradius $6$. Three circles of radius $\frac{p}{q}$, where $p$ and $q$ are relatively prime positive integers, meet at exactly one point, and each is tangent to two distinct sides of triangle $ABC$. Find $p + q$.

We are given a circle and a square in the plane with radius $r$ and side length $s$, respectively. Let $X$ be the locus of points that is a midpoint between some point inside the circle and some point inside the square. If the minimum value of $[X]/rs$, where $[X]$ is the area of region $X$, can be written as $\frac{a+\sqrt{\pi}}{b}$, find $a + b$.

Imagine a paper cutout in the shape of an equilateral triangle that has three other equilateral triangles that each share a distinct side of the original triangle. This shape can be folded up into a tetrahedron. How many such shapes in $2D$ are there that fold into a tetrahedron? Valid shapes must consist of a tessellation of equal sized equilateral triangles, and two shapes are considered the same (and shouldn’t be counted separately) if they can be rotated or flipped to match.

Suppose that $\vartriangle ABC$ has side lengths $AB = 2013$, $AC = 2015$ and $BC = 1007$. Let $P$ be a point inside $\vartriangle ABC$. Let $X$ and $Y$ be the feet of the perpendiculars from $P$ to $AB$ and $AC$ respectively. Suppose that $\angle BPX = \angle CPY$ . Let the perpendicular bisector of $XY$ intersect segment $BC$ at $Q$. If $\left(\frac{BQ}{QC}\right)^2=\frac{a}{b}$ where $a, b$ are coprime positive integers, find $a + b$.

Triangle $ABC$ has $AB=BC=10$ and $CA=16$. The circle $\Omega$ is drawn with diameter $BC$. $\Omega$ meets $AC$ at points $C$ and $D$. Find the area of triangle $ABD$.

The area of parallelogram $ABCD$ is $51\sqrt{55}$ and $\angle{DAC}$ is a right angle. If the side lengths of the parallelogram are integers, what is the perimeter of the parallelogram?

A right regular hexagonal prism has bases $ABCDEF$, $A'B'C'D'E'F'$ and edges $AA'$, $BB'$, $CC'$, $DD'$, $EE'$, $FF'$, each of which is perpendicular to both hexagons. The height of the prism is $5$ and the side length of the hexagons is $6$. The plane $P$ passes through points $A$, $C'$, and $E$. The area of the portion of $P$ contained in the prism can be expressed as $m\sqrt{n}$, where $n$ is not divisible by the square of any prime. Find $m+n$.

An equilateral triangle $ABC$ has side length $7$. Point $P$ is in the interior of triangle $ABC$, such that $PB=3$ and $PC=5$. The distance between the circumcenters of $ABC$ and $PBC$ can be expressed as $\frac{m\sqrt{n}}{p}$, where $n$ is not divisible by the square of any prime and $m$ and $p$ are relatively prime positive integers. What is $m+n+p$?

Rectangle $HOMF$ has $HO=11$ and $OM=5$. Triangle $ABC$ has orthocenter $H$ and circumcenter $O$. $M$ is the midpoint of $BC$ and altitude $AF$ meets $BC$ at $F$. Find the length of $BC$.

Triangle $ABC$ has $\angle{A}=90^{\circ}$, $AB=2$, and $AC=4$. Circle $\omega_1$ has center $C$ and radius $CA$, while circle $\omega_2$ has center $B$ and radius $BA$. The two circles intersect at $E$, different from point $A$. Point $M$ is on $\omega_2$ and in the interior of $ABC$, such that $BM$ is parallel to $EC$. Suppose $EM$ intersects $\omega_1$ at point $K$ and $AM$ intersects $\omega_1$ at point $Z$. What is the area of quadrilateral $ZEBK$?

Let $ACDB$ be a cyclic quadrilateral with circumcenter $\omega$. Let $AC=5$, $CD=6$, and $DB=7$. Suppose that there exists a unique point $P$ on $\omega$ such that $\overline{PC}$ intersects $\overline{AB}$ at a point $P_1$ and $\overline{PD}$ intersects $\overline{AB}$ at a point $P_2$, such that $AP_1=3$ and $P_2B=4$. Let $Q$ be the unique point on $\omega$ such that $\overline{QC}$ intersects $\overline{AB}$ at a point $Q_1$, $\overline{QD}$ intersects $\overline{AB}$ at a point $Q_2$, $Q_1$ is closer to $B$ than $P_1$ is to $B$, and $P_2Q_2=2$. The length of $P_1Q_1$ can be written as $\frac{p}{q}$, where $p$ and $q$ are relatively prime positive integers. Find $p+q$.
Triangle $ABC$ with $AB=4$, $BC=5$, $CA=6$ has circumcircle $\Omega$ and incircle $\omega$. Let $\Gamma$ be the circle tangent to $\Omega$ and the sides $AB$, $BC$, and let $X=\Gamma \cap \Omega$. Let $Y$, $Z$ be distinct points on $\Omega$ such that $XY$, $YZ$ are tangent to $\omega$. Find $YZ^2$.

The following fact may be useful: if $\triangle{ABC}$ has incircle $w$ with incenter $I$ and radius $r$, and $\triangle{DEF}$ is the intouch triangle (i.e. $D$, $E$, $F$ are intersections of incircle with $BC$, $CA$, $AB$, respectively) and $H$ is the orthocenter of $\triangle{DEF}$, then the inversion of $X$ about $\omega$ (i.e. the point $X'$ on ray $IX$ such that $IX' \cdot IX=r^2$) is the midpoint of $DH$.

Equilateral triangle $ABC$ has area $1$. $A'$, $B'$, and $C'$ are the midpoints of $BC$, $CA$, and $AB$, respectively. $A''$, $B''$, $C''$ are the midpoints of $B'C'$, $C'A'$, and $A'B'$, respectively. The area of trapezoid $BB''C''C$ can be written as $\frac{m}{n}$ for relative prime positive integers $m$ and $n$. Find $m+n$.

A kite is inscribed in a circle with center $O$ and radius $60$. The diagonals of the kite meet at a point $P$, and $OP$ is an integer. The minimum possible area of the kite can be expressed in the form $a\sqrt{b}$, where $a$ and $b$ are positive integers and $b$ is squarefree. Find $a+b$.

Triangle $ABC$ has incenter $I$. The line through $I$ perpendicular to $AI$ meets the circumcircle of $ABC$ at points $P$ and $Q$, where $P$ and $B$ are on the same side of $AI$. Let $X$ be the point such that $PX$ // $CI$ and $QX$ // $BI$. Show that $P B, QC$, and $IX$ intersect at a common point.

In regular pentagon $ABCDE$, let $O \in CE$ be the center of circle $\Gamma$ tangent to $DA$ and $DE$. $\Gamma$ meets $DE$ at $X$ and $DA$ at $Y$ . Let the altitude from $B$ meet $CD$ at $P$. If $CP = 1$, the area of $\vartriangle COY$ can be written in the form $\frac{a}{b}  \frac{\sin c^o}{\cos^2 c^o}$ , where $a$ and $b$ are relatively prime positive integers and $c$ is an integer in the range $(0, 90)$. Find $a + b + c$.

A point-sized cue ball is fired in a straight path from the center of a regular hexagonal billiards table of side length $1$. If it is not launched directly into a pocket but travels an integer distance before falling into one of the pockets (located in the corners), find the minimum distance that it could have traveled.
A cylinder has radius $6$ and height $12$. An equilateral triangle is inscribed in both bases of the cylinder, then a triangular prism is removed from the cylinder by drilling perpendicular to the bases through the image of the equilateral triangles. If the surface area of the new figure can be expressed as $a\pi+b\sqrt{c}$ for integers $a, b$, and $c$ (where $c$ is divisible by no perfect squares) then find $a + b + c$.

Kapil the Kingly, Casimir the Conjurer, and Zack the Zombie all stand in clockwise order on the perimeter of a circular hockey rink with radius $10$ meters. The central angle between Kapil and Casimir is $30^o$ and the central angle between Casimir and Zack is $130^o$ . Kapil smacks a hockey puck in a certain direction, and the puck bounces against the edge of the rink without losing velocity. Kapil aims his shot so that it takes the minimal number of bounces to reach both Casimir and Zack. If the total number of meters traveled by the puck when it has reached the final person is a $\sin (b^o)$, where a and b are positive integers and $0 \le b < 90^o$, find $a + b$.

Note: the puck bounces off of the rink according to the rule “angle of incidence equals angle of reflection” with respect to the tangent line.

Points $E$ and $F$ lie on sides $AC$ and $AB$ (respectively) of $\vartriangle ABC$ so that $EF \parallel BC$. Suppose there is a point $P$ on the circumcircle of $\vartriangle ABC$ such that $\angle BPE = \angle CPF = 90^o$ . Given that $AB = 13$, $BC = 14$, and $CA = 15$, the distance from $P$ to line $EF$ can be written in the form $\frac{p}{q}$ where $p$ and $q$ are positive integers with $\gcd (p, q) = 1$. Find $p + q$.

Frist Campus Center is located $1$ mile north and $1$ mile west of Fine Hall. The area within $5$ miles of Fine Hall that is located north and east of Frist can be expressed in the form $\frac{a}{b} \pi - c$, where $a, b, c$ are positive integers and $a$ and $b$ are relatively prime. Find $a + b + c$.

Let $\overline{AD}$ be a diameter of a circle. Let point $B$ be on the circle, point $C$ on $\overline{AD}$ such that $A, B, C$ form a right triangle at $C$. The value of the hypotenuse of the triangle is $4$ times the square root of its area. If $\overline{BC}$ has length $30$, what is the length of the radius of the circle?

Let $\triangle ABC$ satisfy $AB = 17, AC = \frac{70}{3}$ and $BC = 19$. Let $I$ be the incenter of $\triangle ABC$ and $E$ be the excenter of $\triangle ABC$ opposite $A$. (Note: this means that the circle tangent to ray $AB$ beyond $B$, ray $AC$ beyond $C$, and side $BC$ is centered at $E$.) Suppose the circle with diameter $IE$ intersects $AB$ beyond $B$ at $D$. If $BD = \frac{a}{b}$ where $a, b$ are coprime positive integers, find $a + b$.

Triangle $ABC$ has $\angle{A}=90^\circ$, $\angle{C}=30^\circ$, and $AC=12$. Let the circumcircle of this triangle be $W$. Define $D$ to be the point on arc $BC$ not containing $A$ so that $\angle{CAD}=60^\circ$. Define points $E$ and $F$ to be the foots of the perpendiculars from $D$ to lines $AB$ and $AC$, respectively.
Let $J$ be the intersection of line $EF$ with $W$, where $J$ is on the minor arc $AC$. The line $DF$ intersects $W$ at $H$ other than $D$. The area of the triangle $FHJ$ is in the form $\frac{a}{b}(\sqrt{c}-\sqrt{d})$ for positive integers $a,b,c,d,$ where $a,b$ are relatively prime, and the sum of $a,b,c,d$ is minimal. Find $a+b+c+d$.

Let $\triangle BC$ be a triangle with side lengths $AB = 9, BC = 10, CA = 11$. Let $O$ be the circumcenter of $\triangle ABC$. Denote $D = AO \cap BC, E = BO \cap CA, F = CO \cap AB$. If $\frac{1}{AD} + \frac{1}{BE} + \frac{1}{FC}$ can be written in simplest form as $\frac{a \sqrt{b}}{c}$, find $a + b + c$.

Let triangle $ABC$ have $\angle BAC = 45^{\circ}$ and circumcircle $\Gamma$ and let $M$ be the intersection of the angle bisector of $\angle BAC$ with $\Gamma$. Let $\Omega$ be the circle tangent to segments $\overline{AB}$ and $\overline{AC}$ and internally tangent to $\Gamma$ at point $T$. Given that $\angle TMA = 45^{\circ}$ and that $TM = \sqrt{100 - 50 \sqrt{2}}$, the length of $BC$ can be written as $a \sqrt{b}$, where $b$ is not divisible by the square of any prime. Find $a + b$.

Let $ABCD$ be a parallelogram such that $AB = 35$ and $BC = 28$. Suppose that $BD \perp BC$. Let $\ell_1$ be the reflection of $AC$ across the angle bisector of $\angle BAD$, and let $\ell_2$ be the line through $B$ perpendicular to $CD$. $\ell_1$ and $\ell_2$ intersect at a point $P$. If $PD$ can be expressed in simplest form as $\frac{m}{n}$, find $m + n$.

Let $\omega$ be a circle. Let $E$ be on $\omega$ and $S$ outside $\omega$ such that line segment $SE$ is tangent to $\omega$. Let $R$ be on $\omega$. Let line $SR$ intersect $\omega$ at $B$ other than $R$, such that $R$ is between $S$ and $B$. Let $I$ be the intersection of the bisector of $\angle ESR$ with the line tangent to $\omega$ at $R$; let $A$ be the intersection of the bisector of $\angle ESR$ with $ER$. If the radius of the circumcircle of $\triangle EIA$ is $10$, the radius of the circumcircle of $\triangle SAB$ is $14$, and $SA = 18$, then $IA$ can be expressed in simplest form as $\frac{m}{n}$. Find $m + n$.

Let a right cone of the base radius $r=3$ and height greater than $6$ be inscribed in a sphere of radius $R=6$. The volume of the cone can be expressed as $\pi(a\sqrt{b}+c)$, where $b$ is square free. Find $a+b+c$.

Consider rectangle $ABCD$ with $AB=30$ and $BC=60$. Construct circle $T$ whose diameter is $AD$. Construct circle $S$ whose diameter is $AB$. Let circles $S$ and $T$ intersect at $P$ such that $P\neq A$. Let $AP$ intersect $BC$ at $E$. Let $F$ be the point on $AB$ such that $EF$ is tangent to the circle with diameter $AD$. Find the area of triangle $AEF$.

Let $ABC$ be a triangle. Construct three circles $k_1$, $k_2$, and $k_3$ with the same radius such that they intersect each other at a common point $O$ inside the triangle $ABC$ and $k_1\cap k_2=\{A,O\}$, $k_2 \cap k_3=\{B,O\}$, $k_3\cap k_1=\{C,O\}$. Let $t_a$ be a common tangent of circles $k_1$ and $k_2$ such that $A$ is closer to $t_a$ than $O$. Define $t_b$ and $t_c$ similarly. Those three tangents determine a triangle $MNP$ such that the triangle $ABC$ is inside the triangle $MNP$. Prove that the area of $MNP$ is at least $9$ times the area of $ABC$.
Let triangle $\triangle{ABC}$ have $AB=90$ and $AC=66$. Suppose that the line $IG$ is perpendicular to side $BC$, where $I$ and $G$ are the incenter and centroid, respectively. Find the length of $BC$.

Let triangle $\triangle{MNP}$ have side lengths $MN=13$, $NP=89$, and $PM=100$. Define points $S$, $R$, and $B$ as the midpoints of $\overline{MN}$, $\overline{NP}$, and $\overline{PM}$ respectively. A line $\ell$ cuts lines $\overline{MN}$, $\overline{NP}$, and $\overline{PM}$ at points $I$, $J$, and $A$ respectively. Find the minimum value of $(SI+RJ+BA)^2.$

In right triangle $\triangle{ABC}$, a square $WXYZ$ is inscribed such that vertices $W$ and $X$ lie on hypotenuse $\overline{AB}$, vertex $Y$ lies on leg $\overline{BC}$, and vertex $Z$ lies on leg $\overline{CA}$. Let $\overline{AY}$ and $\overline{BZ}$ intersect at some point $P$. If the length of each side of square $WXYZ$ is $4$, the length of the hypotenuse $\overline{AB}$ is $60$, and the distance between point $P$ and point $G$, where $G$ denotes the centroid of $\triangle{ABC}$, is $\tfrac{a}{b}$, compute the value of $a+b$.

Aaron the Ant is somewhere on the exterior of a hollow cube of side length $2$ inches, and Fred the Flea is on the inside, at one of the vertices. At some instant, Fred flies in a straight line towards the opposite vertex, and simultaneously Aaron begins crawling on the exterior of the cube towards that same vertex. Fred moves at $\sqrt{3}$ inches per second and Aaron moves at $\sqrt{2}$ inches per second. If Aaron arrives before Fred, the area of the surface on the cube from which Aaron could have started can be written as $a\pi+\sqrt{b}+c$ where $a$, $b$, and $c$ are integers. Find $a+b+c.$

Let $ABC$ be a triangle with side lengths $13,14,15$. The points on the interior of $ABC$ with distance at least $1$ from each side are shaded. The area of the shaded region can be written in simplest form as $\tfrac{m}{n}$. Find $m+n$.

Some number of regular polygons meet at a point on the plane such that the polygons' interiors do not overlap, but the polygons fully surround the point (i.e. a sufficiently small circle centered at the point would be contained in the union of the polygons). What is the largest possible number of sides in any of the polygons?

Kite $ABCD$ has right angles at $B$ and $D$, and $AB<BC$. Points $E\in AB$ and $F\in AD$ satisfy $AE=4$, $EF=7$, and $FA=5$. If $AB=8$ and points $X$ lies outside $ABCD$ while satisfying $XE-XF=1$ and $XE+XF+2XA=23$, then $XA$ may be written as $\tfrac{a-b\sqrt{c}}{d}$ for $a,b,c,d$ positive integers with $\gcd(a^2,b^2,c,d^2)=1$ and $c$ squarefree. Find $a+b+c+d$.

The triangle $ABC$ satisfies $AB=10$ and has angles $\angle{A}=75^{\circ}$, $\angle{B}=60^{\circ}$, and $\angle C = 45^{\circ}$. Let $I_A$ be the center of the excircle opposite $A$, and let $D$, $E$ be the circumcenters of triangle $BCI_A$ and $ACI_A$ respectively. If $O$ is the circumcenter of triangle $ABC$, then the area of triangle $EOD$ can be written as $\tfrac{a\sqrt{b}}{c}$ for square-free $b$ and coprime $a,c$. Find the value of $a+b+c$.




A right cone in $xyz$-space has its apex at $(0,0,0)$, and the endpoints of a diameter on its base are $(12,13,-9)$ and $(12,-5,15)$. The volume of the cone can be expressed as $a\pi$. What is $a$?

2019 PUMaC Geometry A2 / B3
Let $\triangle ABC$ be a triangle with circumcenter $O$ and orthocenter $H$. Let $D$ be a point on the circumcircle of $ABC$ such that $AD \perp BC$. Suppose that $AB = 6, DB = 2$, and the ratio $\tfrac{\text{area}(\triangle ABC)}{\text{area}(\triangle HBC)}=5.$ Then, if $OA$ is the length of the circumradius, then $OA^2$ can be written in the form $\tfrac{m}{n}$, where $m$ and $n$ are relatively prime positive integers. Compute $m + n$.

2019 PUMaC Geometry A3 / B4
Suppose we choose two numbers $x,y\in[0,1]$ uniformly at random. If the probability that the circle with center $(x,y)$ and radius $|x-y|$ lies entirely within the unit square $[0,1]\times [0,1]$ is written as $\tfrac{p}{q}$ with $p$ and $q$ relatively prime nonnegative integers, then what is $p^2+q^2$

Let $BC=6$, $BX=3$, $CX=5$, and let $F$ be the midpoint of $\overline{BC}$. Let $\overline{AX}\perp\overline{BC}$ and $AF=\sqrt{247}$. If $AC$ is of the form $\sqrt{b}$ and $AB$ is of the form $\sqrt{c}$ where $b$ and $c$ are nonnegative integers, find $2c+3b$.

2019 PUMaC Geometry A5 / B6
Let $\Gamma$ be a circle with center $A$, radius $1$ and diameter $BX$. Let $\Omega$ be a circle with center $C$, radius $1$ and diameter $DY $, where $X$ and $Y$ are on the same side of $AC$. $\Gamma$ meets $\Omega$ at two points, one of which is $Z$. The lines tangent to $\Gamma$ and $\Omega$ that pass through $Z$ cut out a sector of the plane containing no part of either circle and with angle $60^\circ$. If $\angle XY C = \angle CAB$ and $\angle XCD = 90^\circ$, then the length of $XY$ can be written in the form $\tfrac{\sqrt a+\sqrt b}{c}$ for integers $a, b, c$ where $\gcd(a, b, c) = 1$. Find $a + b + c$. 

Let two ants stand on the perimeter of a regular $2019$-gon of unit side length. One of them stands on a vertex and the other one is on the midpoint of the opposite side. They start walking along the perimeter at the same speed counterclockwise. The locus of their midpoints traces out a figure $P$ in the plane with $N$ corners. Let the area enclosed by the convex hull of $P$ be $\tfrac{A}{B}\tfrac{\sin^m\left(\tfrac{\pi}{4038}\right)}{\tan\left(\tfrac{\pi}{2019}\right)}$, where $A$ and $B$ are coprime positive integers, and $m$ is the smallest possible positive integer such that this formula holds. Find $A+B+m+N$.

Note: The convex hull of a figure $P$ is the convex polygon of smallest area which contains $P$.

Let $ABCD$ be a trapezoid such that $AB||CD$ and let $P=AC\cap BD,AB=21,CD=7,AD=13,[ABCD]=168.$ Let the line parallel to $AB$ through $P$ intersect the circumcircle of $BCP$ in $X.$ Circumcircles of $BCP$ and $APD$ intersect at $P,Y.$ Let $XY\cap BC=Z.$ If $\angle ADC$ is obtuse, then $BZ=\frac{a}{b},$ where $a,b$ are coprime positive integers. Compute $a+b.$

Let $\gamma$ and $\Gamma$ be two circles such that $\gamma$ is internally tangent to $\Gamma$ at a point $X$. Let $P$ be a point on the common tangent of $\gamma$ and $\Gamma$ and $Y$ be the point on $\gamma$ other than $X$ such that $PY$ is tangent to $\gamma$ at $Y$. Let $PY$ intersect $\Gamma$ at $A$ and $B$, such that $A$ is in between $P$ and $B$ and let the tangents to $\Gamma$ at $A$ and $B$ intersect at $C$. $CX$ intersects $\Gamma$ again at $Z$ and $ZY$ intersects $\Gamma$ again at $Q$. If $AQ = 6, AB = 10$ and $\tfrac{AX}{XB} = \tfrac{1}{4}$. The length of $QZ = \tfrac{p}{q}\sqrt{r}$ where $p$ and $q$ are coprime positive integers, and $r$ is square free positive integer. Find $p + q + r$.

Suppose we have a convex quadrilateral $ABCD$ such that $\angle B = 100^\circ$ and the circumcircle of $\triangle ABC$ has a center at $D$. Find the measure, in degrees, of $\angle D$.

 Note: The circumcircle of a $\triangle ABC$ is the unique circle containing $A$, $B$, and $C$.

 Let $ABCDEF$ be a convex hexagon with area $S$ such that $AB \parallel DE$, $BC \parallel  EF$, $CD \parallel  FA$ holds, and whose all angles are obtuse and opposite sides are not the same length. Prove that the following inequality holds:$$A_{ABC} + A_{BCD} + A_{CDE} + A_{DEF} + A_{EFA} + A_{FAB} < S$$, where $A_{XYZ}$ is the area of triangle $XYZ$

Let $MN$ be a chord of the circle $\Gamma$ and let $S$ be the midpoint of $MN$. Let $A, B, C, D$ be points on $\Gamma$ such that $AC$ and $BD$ intersect at $S$ and $A$ and $B$ are on the same side of $MN$. Let $d_A, d_B, d_C , d_D$ be the distances from $MN$ to $A, B, C,$ and $D,$ respectively. Prove that $\frac{1}{d_A}+\frac{1}{d_D}=\frac{1}{d_B}+\frac{1}{d_C}$.

Let $f(x) = x^3 + 3x^2 + 1$. There is a unique line of the form $y = mx + b$ such that $m > 0$ and this line intersects $f(x)$ at three points, $A, B, C$ such that $AB = BC = 2$. Find $\lfloor 100m \rfloor$.
The curves $y = x + 5$ and $y = x^2 - 3x$ intersect at points $A$ and $B$. $C$ is a point on the lower curve between $A$ and $B$. The maximum possible area of the quadrilateral $ABCO$ can be written as $A/B$ for coprime $A, B$. Find $A + B$.

In quadrilateral $ABCD$, angles $A, B, C, D$ form an increasing arithmetic sequence. Also, $\angle ACB = 90^o$ . If $CD = 14$ and the length of the altitude from $C$ to $AB$ is $9$, compute the area of $ABCD$.

Let right triangle $ABC$ have hypotenuse $AC$ and $AB = 8$. Let $D$ be the foot of the altitude from $B$ to $AC$. If $ABC$ has area $60$, then the length of $BD$ can be expressed in the form $\frac{a}{b}$, where $a$ and $b$ are relatively prime, positive integers. Find $a + b$.

Consider a triangle where the sum of the three side lengths is equal to the product of the three side lengths. If the circumcircle has $25$ times the area of the incircle, the distance between the incenter and the circumcenter can be expressed in the form $\frac{\sqrt{x}}{y}$ , for integers $x$ and $y$, with $x$ square-free. Find $x + y$.

In $ \vartriangle ABC$, let $\angle CAB = 45$ deg, and $|AB| =\sqrt2$, $|AC| = 6$. Let $M$ be the midpoint of side $BC$. The line $AM$ intersects the circumcircle of $ \vartriangle ABC$ at $ P$. The circle centered at $M$ with radius $ MP$ intersects the circumcircle of $ABC$ again at $Q \ne P$. Suppose the tangent to the circumcircle of $ \vartriangle ABC$ at $ B$ intersects $AQ$ at $T$. Find $TC^2$.



185

Let $\gamma_1$ and $\gamma_2$ be circles centered at $O$ and $ P$ respectively, and externally tangent to each other at point $Q$. Draw point $D$ on $\gamma_1$ and point $E$ on $\gamma_2$ such that line $DE$ is tangent to both circles. If the length $OQ = 1$ and the area of the quadrilateral $ODEP$ is $520$, then what is the value of length $PQ$?

Hexagon $ABCDEF$ has an inscribed circle $\Omega$ that is tangent to each of its sides. If $AB = 12$, $\angle FAB = 120^o$, and $\angle ABC = 150^o$, and if the radius of $\Omega$ can be written as $m +\sqrt{n}$ for positive integers $m, n$, find $m + n$.

Let $ABCD$ be a cyclic quadrilateral with circumcenter $O$ and radius $10$. Let sides $AB$, $BC$, $CD$, and $DA$ have midpoints $M, N, P$, and $Q$, respectively. If $MP = NQ$ and $OM + OP = 16$, then what is the area of triangle $\vartriangle OAB$?

Let $C$ be a circle centered at point $O$, and let $P$ be a point in the interior of $C$. Let $Q$ be a point on the circumference of $C$ such that $PQ \perp OP$, and let $D$ be the circle with diameter $PQ$. Consider a circle tangent to $C$ whose circumference passes through point $P$. Let the curve $\Gamma$ be the locus of the centers of all such circles. If the area enclosed by $\Gamma$ is $1/100$ the area of $C$, then what is the ratio of the area of $C$ to the area of $D$?

Triangle $ABC$ is so that $AB = 15$, $BC = 22$, and $AC = 20$. Let $D, E, F$ lie on $BC$, $AC$, and $AB$, respectively, so $AD$, $BE$, $CF$ all contain a point $K$. Let $L$ be the second intersection of the circumcircles of $BFK$ and $CEK$. Suppose that $\frac{AK}{KD} = \frac{11}{7}$ , and $BD = 6$. If $KL^2 =\frac{a}{b}$, where $a, b$ are relatively prime integers, find $a + b$.

Triangle $ABC$ has side lengths $13$, $14$, and $15$. Let $E$ be the ellipse that encloses the smallest area which passes through $A, B$, and $C$. The area of $E$ is of the form $\frac{a \sqrt{b}\pi}{c}$ , where $a$ and $c$ are coprime and $b$ has no square factors. Find $a + b + c$.

Let $ABC$ be a triangle with sides $AB = 34$, $BC = 15$, $AC = 35$ and let $\Gamma$ be the circle of smallest possible radius passing through $A$ tangent to $BC$. Let the second intersections of $\Gamma$ and sides $AB$, $AC$ be the points $X, Y$ . Let the ray $XY$ intersect the circumcircle of the triangle $ABC$ at $Z$. If $AZ =\frac{p}{q}$ for relatively prime integers $p$ and $q$, find $p + q$.

$A_1A_2A_3A_4$ is a cyclic quadrilateral inscribed in circle $\Omega$, with side lengths $A_1A_2 = 28$, $A_2A_3 =12\sqrt3$, $A_3A_4 = 28\sqrt3$, and $A_4A_1 = 8$. Let $X$ be the intersection of $A_1A_3, A_2A_4$. Now, for $i = 1, 2, 3, 4$, let $\omega_i$ be the circle tangent to segments$ A_iX$, $A_{i+1}X$, and $\Omega$, where we take indices cyclically (mod $4$). Furthermore, for each $i$, say $\omega_i$ is tangent to $A_1A_3$ at $X_i $, $A_2A_4$ at $Y_i$ , and $\Omega$ at $T_i$ . Let $P_1$ be the intersection of $T_1X_1$ and $T_2X_2$, and $P_3$ the intersection of $T_3X_3$ and $T_4X_4$. Let $P_2$ be the intersection of $T_2Y_2$ and $T_3Y_3$, and $P_4$ the intersection of $T_1Y_1$ and $T_4Y_4$. Find the area of quadrilateral $P_1P_2P_3P_4$.

You are walking along a road of constant width with sidewalks on each side. You can only walk on the sidewalks or cross the road perpendicular to the sidewalk. Coming up on a turn, you realize that you are on the “outside” of the turn; i.e., you are taking the longer way around the turn. The turn is a circular arc. Assuming that your destination is on the same side of the road as you are currently, let $\theta$ be the smallest turn angle, in radians, that would justify crossing the road and then crossing back after the turn to take the shorter total path to your destination. What is $\lfloor 100 \cdot \theta \rfloor$ ?

Seven students in Princeton Juggling Club are searching for a room to meet in. However, they must stay at least $6$ feet apart from each other, and due to midterms, the only open rooms they can find are circular. In feet, what is the smallest diameter of any circle which can contain seven points, all of which are at least $6$ feet apart from each other?

Helen has a wooden rectangle of unknown dimensions, a straightedge, and a pencil (no compass). Is it possible for her to construct a line segment on the rectangle connecting the midpoints of two opposite sides, where she cannot draw any lines or points outside the rectangle?

Note: Helen is allowed to draw lines between two points she has already marked, and mark the intersection of any two lines she has already drawn, if the intersection lies on the rectangle. Further, Helen is allowed to mark arbitrary points either on the rectangle or on a segment she has previously drawn. Assume that only the four vertices of the rectangle have been marked prior to the beginning of this process.

Let $ABC$ be a triangle and let the points $D, E$ be on the rays $AB$, $AC$ such that $BCED$ is cyclic. Prove that the following two statements are equivalent:
$\bullet$ There is a point $X$ on the circumcircle of $ABC$ such that $BDX$, $CEX$ are tangent to each other.
$\bullet$ $AB \cdot AD \le 4R^2$, where $R$ is the radius of the circumcircle of $ABC$.

Let $X, Y$ , and $Z$ be concentric circles with radii $1$, $13$, and $22$, respectively. Draw points $A, B$, and $C$ on $X$, $Y$ , and $Z$, respectively, such that the area of triangle $ABC$ is as large as possible. If the area of the triangle is $\Delta$, find $\Delta^2$.


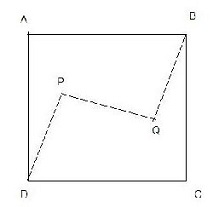
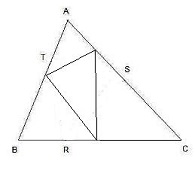
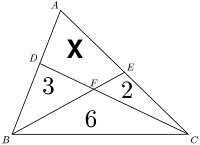
No comments:

Post a Comment

Subscribe to: Posts (Atom)