geometry problems from Rio de Janeiro Mathematical Olympiad (OMERJ) with aops links in the names
Olimpíada de Matemática do Estado do Rio de Janeiro
collected inside aops here
1998 - 2020
The points $C$ and $D$ lie pn a semicircle of diameter AB as shown in the figure below:
https://cdn.artofproblemsolving.com/attachments/d/0/bace71f90c2299a042197488e2a0f75dbebc37.png
The points $C$ and $D$ can move on a semicircle, such that arc $CD$ is always constant and equal to $70^o$.
a) Explain why line $EF$ is always perpendicular to $AB$.
b) Calculate the angles $AEB$ and $AFB$.
c) Determine the set of points $E$ when the points $C$ and $D$ move along the semicircle.
A trapezoid $ABCD$ with bases $BC$ and $AD$ with $BC < AD$ is such that and $2AB=CD$ and $\angle BAD+\angle CDA=120^o$. Determine the angles of the trapezoid $ABCD$.
In a triangle $ABC$ where the angle $\angle BAC$ is equal to $60^o$, choose a point from its interior so that the angles $\angle APB$, $\angle BPC$ and $\angle CPA$ are equal to $120°$. If $AP = a$, find the area of the triangle $BPC$.
Triangle $ABC$ is equilateral with side $a$. On side $AB$, point $P$ is marked, such that $AP=b$ (where $b <a$ ), and on the extension of the side $BC$, point $Q$ is marked (closer to $C$ than to $ B$) such that $CQ=b$ . The segment $PQ$ cuts the side $AC$ at point $M$.
1) Prove that $M$ is the midpoint of $PQ$.
2) Calculate the ratio of the areas of the triangles $APM$ and $MCQ$.
PS. Level 2 asked only for 1. level 3 asked for both 1 and 2.
Inside a rectangle $ABCD$ we have $2$ circles, one tangent to sides $AB$ and $AD$, the other tangent to sides $BC$ and $CD$. Both are also tangent to each other. Prove that the distance between the centers only depends on the lengths of the sides of the rectangle.
Let $I$ be the intetrsection point of the internal bisectors of a triangle $ABC$. Let $ r$ be the line perpendicular to $AI$ passing through $A$. Let $s$ be the line perpendicular to $CI$ passing through $C$. Let $P$ be the intersection point of $ r$ and $s$. Prove that $B,P,I$ are collinear.
Two little ants, mother and daughter, walk from point A to point B on a wire frame in circular shape and negligible dimensions for analysis. Exists another frame similar, external and concentric to the first one where the little ants walked.
The two engage in the following dialogue:
- Daughter: Μother! Wouldn't it be better to walk to the other frame, walk through it to a certain point and then back to the frame we're in? The way wouldn't it be shorter?
- Mother: Look my daughter, this is correct for some center angles, but wrong for others.
For which range of angles the child's proposal is valid and for which range it is doesn't suit?
Note: The transfer between the circles is done so that the path is perpendicular to two imaginary lines, each externally tangent to the one circle.
Given a triangle $ABC$, let $A_1$ be the foot of the altitude relative to the side $BC$, $A_2$ and $A_3$ be the orthogonal projections of $A_1$ over $AC$ and $AB$, respectively. Let $B_3$ be the foot of the altitude relative to side $AC$, $B_2$ and $B_3$ be the orthogonal projections of $B_3$ on $BC$ and $AB$, respectively. Let $C_1$ be the foot of the altitude relative to side $AB$, $C_2$ and $C_3$ be the orthogonal projections of $C_1$ on $AC$ and $BC$, respectively. Prove that the points $A_2$, $A_3$ , $B_2$ , $B_3$, $C_2$, $C_3$ lie on the same circle.
The figure represents the $1/4$ part of a circle of radius $ 1$. In arc $AB$ we consider two points$ P$ and $Q$ such that the line $PQ$ is parallel to the line $AB$. Let $X$ and $Y$ be the intersection points of the line $PQ$ with the lines $AO$ and $OB$ respectively. Calculate $PX^2 + PY^2$.
Given a triangle $XYZ$, the triangle $X’Y’Z’$ is called "son" of $XYZ$, such that $X’$ lies on $YZ$, $Y’$ lies on $XZ$, $Z’$ lies on $XY$ and $XZ’ = 2YZ’$, $ZY’ = 2XY’$ and $YX’ = 2ZX’$. Given a triangle $ABC$, let $A_1B_1C_1$ be it's son, let $A_2B_2C_2$ be the son of $A_1B_1C_1$, and, more generally, let $A_{n+1}B_{n+1}C_{n+1}$ be the son of $A_nB_nC_n$. Prove that the centroid of triangle $ABC$ lies on the interior of triangle $A_nB_nC_n$ for every positive integer $n$.
Let $ABC$ be a right triangle at $A$ and $M, N$ points on the side $BC$ such that $BM=MN=CN$. If $AM=3$ and $AN=2$, calculate the length of $MN$.
$ABC$ is an acute-angled triangle of base $AB=b$ and altitude $CH=h$. Infinite squares are constructed within $ABC$ such that each square has two of its vertices on the sides $BC$ and $CD$ of the triangle and the other two vertices lies on the previous square (the first square's lie on $AB$).
a) What is the sum of the areas of all squares, in terms of $b$ and $h$ ?
b) What is the largest possible ratio between the area of the first square and the area of the triangle?
Two circles, $\Gamma_1$ and $\Gamma_2$, intersect at $A$ and $ B$. Two other circles, $\Gamma_3$ and $\Gamma_4$ , tangent internally to $\Gamma_1$ at $A$ and $ B$ , respectively, cut again $\Gamma_2$ at $ P$ and $Q$, respectively. Suppose the tangent lines to $\Gamma_3$ and $\Gamma_4$, at $ P$ and $Q$ intersect at one point $R$. Prove that $PR=QR$.
Consider a regular hexagon $H$ of area $18$.
a) Determine how many triangles are there with vertices at the vertices of $H$ .
b) Calculate the sum of the areas of these triangles.
Consider an ellipse of semi-axes $a$ and $b$. Let $A$ be the maximum area value that can have a triangle inscribed in this ellipse. Calculate $A$.
Given a semicircle with center at $O$ and diameter $AB$, and inside it another semicircle with diameter $OA$. Through a point $C$ on $OA$, a straight line perpendicular to the radius $OA$ , cuts the small semicircle at $D$ and the large at $E$. Finally, the straight line $AD$ cuts the large semicircle at $F$. Prove that the circle circumscribed around the triangle $DEF$ is tangent to the chord $AE$ at point $E$ .
In the figure,, the triangle $PQR$ is right at $P$, $AP=3$, $PB=4$ and the segment $AB$ is perpendicular to both the lines $AQ$ and $BR$.
a) Find, in terms of the angle $\theta$, the area of the triangle $PQR$ .
b) Find the smallest value that the area of the triangle $PQR$ can take, when $0^o<\theta<90^o.$
Let $H$ and $O$ be the orthocenter and the circuncenter of triangle $ABC$ respectively,$N$ is the midpoint of $BC$, $D$ is the feet of the altitude on side $BC$.It's given that $HOND$ is a rectangle and $HO=11$ and $ON=5$ find the lenght of $BC$
Consider an hyperbola $H$ , with asymptotes $r ,s$ and focuses $F,F'$. Let $M$ be any point of $H$ and$ t$ be the tangent line of $H$ at $M$. If $P=r \cap t$ and $Q=s \cap t$, prove that $P,Q,F,F'$ lie on the same circle.
Given an rectangle $ABCD$, the points $M$ and $N$ lie on sides $AB$ and $BC$ respectively. The segments $DN$, $DM$ ,$CM$, $AN$ cut the polygon, dividing it into eight parts. We also know that:
$\bullet$ Let $C$ be the point where the segments $DN$ and $CM$ intersect. $2$ units is the area of the triangle $CXN$ .
$\bullet$ Let $Y$ be the point where the segments $CM$ and $AN$ intersect,. $9$ units is the area of the quadrilateral $MYNB$.
$\bullet$ Let $Z$ the point where the segments $DM$ and $AN$ intersect. $3$ units is the area of the triangle $AZM$.
Calculate the area of the triangle $DMN$ that does not belong to any of the triangles $CMB$ and $ABN$.
Let $O$ be the center of the circle circumscribed around a triangle $ABC$. Let $S_1$, $S_2$, $S_3$ respectively be the areas of the triangles $ABO$, $ACO$, $BCO$. Show that there is a triangle whose sides are numerically equal to $S_1$, $S_2$, $S_3$ .
Consider a n-gon equiangular but not equilateral (having equal angles but at least two different sides). Let $P$ be a point inside the polygon . Show that the sum of the distances from $P$ to the sides of the polygon is independent of the position of $P$ inside the polygon.
PS. N3 asked for a pentagon, while N4 asked for a polygon.
$ABCD$ is an isosceles trapezoid with small base $AB$ and $O$ is the intersection point of its diagonals. Point $O$ is also the focus of a parabola that passes through the $4$ vertices of the trapezoid. if $AO = 3OC$ , find $\angle AOB$.
In a triangle $ABC$, the medians drawn from vertices $B$ and $C$ are perpendicular. Prove that the sum of cotangents of angles $B$ and $C$ of the triangle is greater than or equal to $\frac23$ .
Let $A, B, C$ and $D$ be points in space such that the angles $\angle BAD$, $\angle BCD$, $\angle ADC$, $\angle ABC$ are right. Prove that $A, B, C$ and $D$ are coplanar.
Consider an ellipse $H$ with foci $F$ and $F’$ and a point $M$ on $H$ . Determine the locus of the center of the circle ex-scribed in triangle $MFF’$ with respect to side $MF$ when $M$ varies over $H$
Let $ABCD$ be a rectangle with $AB=2 BC$ and $L$ be a point on segment $AB$. Let M and N be the midpoints of segments $AD$ and $BC$ respectively. If the perimeter of $ABCD$ is $144$ cm, determine the area of the quadrilateral $ABNM$ that does not belong to the triangle $LCD$.
Let $ABCD$ be a square of side $4$ and a point of side $AB$ such that $\frac{PA}{PB}= 3$. Determine the common area of the square with the circle of center $P$ and radius $2.$
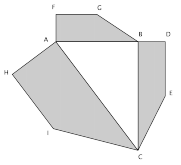
Mr. Manuel bought a piece of land and intends to divide it into three parts, as shown in the figure below, to plant roses, orchids and daisies. The land he bought, $ABCD$, is shaped like a square of side $1$ and we know that $EF=FC=FB$ and $DE=1/2$. What is the area of the triangle $BCF$ intended for planting orchids?
Let $ABC$ be a triangle with circumcircle $\Gamma$ . Let $D$, $E$ and $F$ be the midpoints of $BC$, $AC$ and $AB$ respectively. Let $ r$ be the tangent line to $\Gamma$ at $A$ and $Q$ , $P$ the intersection points of $DE$, $DF$ with $ r$. Let also $S , R$ be the intersections of $PB$ , $QC$ with $\Gamma$ . Prove that $ r$, $RS$ and $BC$ are concurrent.
Consider a parabola $U$ and a fixed angle $\alpha$. Let $P$ be a variable point and $PA$ ,$ PB$ tangents of $U$, with $A, B$ in $U$. If $\angle APB = \alpha$, find the locus of $P$.
Let $ABC$ be a triangle, right at $A$ and $M$ be the midpoint of $BC$. Let $r$ and $s$ be two straight perpendicular lines that intersect at $M$. These lines intersect $AC$ and $AB$ at $R$ and $S$ respectively. Determine the minimum value of length of $RS$ in terms of of $BC$.
Consider an angle $XOY$ and a variable circle tangent to this angle at points $A$ and $B$ ($A \in OX$, $B \in OY$). Consider a fixed point $C$ on the ray $OX$. Tangents to this circle drawn from $C$ touch it at points $A$ and $D$. Prove that line $BD$ passes through a fixed point when the circle varies.
Let $L$ be an ellipse of foci $F$ and $F’$. Let $M$ be a variable point of the ellipse. We define $\theta (M)$ as the acute angle between $MF$ and the tangent line of the ellipse at $M$. Let $\alpha$ be the smallest possible value of $\theta (M)$ when $M$ moves along the ellipse, determine the eccentricity of $L$ in terms of $\alpha$ .
In the following figure, each side of a right triangle $ABC$ corresponds to the larger base of a right trapezoid. Knowing that these trapezoids are similar, that $AB = 4$, $AC = 5$, $AH = FG =2$, $HI =5/2$ and that the trapezoid $BCDE$ has area $9/2$, determine the length of $AF$.
Let $ABC$ be a triangle with $AB \ne AC$ and $D$ the foot of the angle bisector drawn from vertex $A$. Let $\Gamma$ be the circle circumscribed to $ABC$ and $P$ the point where the tangent line of $\Gamma$ at $A$ meets the line $BC$. Finally, let $E$ be the intersection point of the bisector of angle $APB$ with side $AB$. Prove that $DE$ is parallel to $AC$,
Let $P$ be a parabola. Find the locus of points $Q$ such that there are two lines tangent to $P$ by $Q$ and the distances from $Q$ to the touchpoints of each of these lines are equal.
a) Consider a trapezoid $XYWZ$ , where $P$ is the intersection point of its diagonals. If $XY$ and $ZW$ are the bases of this trapezoid, show that the areas of the triangles $XPW$ and $YPZ$ are equal.
b) Now consider a trapezoid $ABCD$ of bases $AB$ and $CD$. Point $E$ is on the $CD$ side and $AE$ is parallel to $BC$. The areas of the triangles $ABQ$ and $ADQ$ are respectively equal to $2$ m$^2$, and $3$ m$^2$, where $Q$ is the intersection point of $BD$ and $AE$. What is the area of the quadrilateral $BCEQ$ ?
Let $ABC$ be a triangle. Let $D$ and $E$ be points on the side $BC$ such that $2BD = 2DE = EC$. Knowing that the circles inscribed in the triangles $ABD$, $ADE $and $AEC$ have the same radius, calculate the sine of the angle $ACB$.
Consider an isosceles trapezoid and two circles as illustrated in the figure below. Find the length of the segment $AB$ that connects the centers of the circles.
Let $A, B$, and $C$ be points on a line with $B$ between $ A$ and $C,$ so that $BC <AB$. Build up
the squares $ABDE$ and $BCFG $ on the same side of the line.
(a) Calculate the ratio $\frac {EF} {AG}.$
(b) Calculate the sum of $\angle BAG + \angle GFE.$
(c) Prove that the $AG, EF$ and $DC $ lines compete on a single point.
The following figure shows two circles that intersect at points $A$ and $B$. Also, note that the larger circle passes through the center of the smaller circle. Let $C$ be a point on the arc $AB$. The line containing points $A$ and $C$ intersects the smallest circle at point $D$. Show that $CD = CB$.
Given a circle $\Gamma$, a secant line $\ell$ of $\Gamma$ at $B , C$ and $r$ a tangent of $\Gamma$ passing through $B$. Take a point $A$ on $\ell$ other than $C$ , such that $AB = BC$. Let $s$ be the tangent of $\Gamma$ passing through $A$. Let $P$ be the intersection point of $r$ and $s$. Proves that angle $\angle APB$ is not obtuse.
Let $ABC$ be an acute triangle with $AB \ne AC$. A point $P$ inside the triangle is said $ B$-good if $\angle PBC = \angle PCA$, it is called $C$-good if $\angle PCB = \angle PBA$. Let $D$ be the $ B$-good point closest to $A$ and $E$ is the closest $C$-good point to $ A$. Let $F$ be the intersection point between the lines $BD$ and $CE$, and $G$ be the intersection point, distinct from $F$, between the circumcircles of $BEF$ and $CDF$.
(a) Prove that the line $PQ$ is perpendicular to the line $BC$.
(b) Prove that $A, E, D$ and $G$ are concyclic.
Let $ABCD$ be a square.$CDE$ and $BFG$ are equilateral triangles such that $B$ is midpoint of $AF$ , $CDE$ is outside the square and $G$ , $ E$ are on the same half-plane determined by line $AB$.
(a) Prove that $DBGE$ is a parallelogram.
(b) Calculate the angles of triangle of $ECG$
Let $ABCD$ be a parallelogram and $P$ be a point on the side $CD$ . Let $Q$ be the intersection point of the line $AP$ with line $BC$ and $F$ the intersection point of line $QD$ with line $AB$. Prove that $PQ = AB$ if, and only if, $PF$ is bisector of the angle $\angle DPA$.
Let $ABC$ be a triangle such that $\angle BAC = 60^o$. Suppose the circumcenter $O$ lies on the circle inscribed in the triangle $ABC$ and $AC > AB$. Prove that $\angle ABC < 84^o$.
In a triangle $ABC$, the angle $BAC$ is twice the angle $\angle ACB$ . Consider a point $D$, on the segment $AC$, such the angle $\angle DBA$ is twice the angle $\angle BAD$ . Calculate the measure of the angle $ACB$, knowing that the measure of the segment $CD$ is equal to $2 BD+AD$.
Let $\Gamma$ be a circle with center $O$ and let $P$ be a point inside $\Gamma$. let $O'$ be the point such that $P$ is midpoint of $O'O$. Suppose the circle $\Gamma'$ with center $O'$ passing though $P$ intersects $\Gamma$ and let $A$ be a intersection point of $\Gamma$ with $\Gamma'$. . If $B'$ is the other intersection point of line $AP$ with $\Gamma$, calculate the ratio $\frac{PB}{PA}$.
In a triangle $ABC$ the point $P$ lies on segment $AB$ such that $AP = 4 PB$. The perpendicular bisector of $PB$ intersects the side $BC$ at point $Q$. Knowing that the area of $PQC$ is $4$, the area of $ABC$ is $25$ and $AC= 10$. Determine the length of $BC$
Let $ABCD$ be a rectangle with sides $AB = 6$ and $BC = 8$. For a point $X$ on side $AB$ with $AX < XB$, draw a line parallel to $BC$. This straight line, together with the diagonals and the sides of the rectangle, will determine $3$ quadrilaterals. Knowing that the sum of the areas of these quadrilaterals is the largest possible, calculate the length of the segment $AX$.
Let $\Gamma$ be a circle with center $O$ and $\ell$ a line tangent to $\Gamma$ at $A$. Let $ B$ be a point on $\Gamma$ (different from the point diametrically opposite to $A$ on $\Gamma$) and let $B'$ be the symmetric of $ B$ wrt $\ell$. Let point $E$, different from $A$, be the intersection of $\Gamma$ with the line$ B'A$ and point $D$, different from $E$, be the intersection of the circles circumscribed around the triangles $BB'E$ and $AOE$.
(a) Calculate the measure of the angle $\angle B'BE$ .
(b) Prove that $B$, $O$ and $D$ are collinear.
Let $ABCD$ be a parallelogram. By a dot $ x$ on the $\overline {AB}$ with $\overline {AX} <\overline{XB}$, draw a line parallel to $\overline{BC}$. This line, along with the diagonals and sides of the parallelogram, will determine $3$ quads. Knowing that the sum of the areas of these quads is as large as possible, calculate the ratio $\frac{\overline{AX}} {\overline{AB}}$
Let ABC be a triangle rectangle acutangle and let $\overline{ AD}$, with D in $\overline{BC}$, be a height relative to point $A$. Let $\gamma_1$ and $\gamma_2$ as circumferences circumscribed to triangles $ABD$ and $ACD$, respectively. The circumference $\gamma_1$ crosses the $AC$ side at points $ A$ and $P$, while $\gamma_2$ crosses the $AB$ side at points $B$ and $Q$. Let $X$ or line intersection point $ BP$ with $\gamma_2$ so that $P$ is between $B$ and $X$. Likewise, be $Y$ the intersection point of the line $QC$ with $\gamma_1$ so that $ Q $ is between $C$ and $Y$. Knowing that $A, X$ and $Y$ are collinear, calculate the smallest possible value to measure the $\angle{BAC}$ angle.
Given an square $ABCD$ of area $104$ . Outside the square is constructed a semicircle of diameter $AB$ . Let $E$ be a point on the semicircle such that $\angle BAE=30^o$. $DE$ intersects $AB$ at point $F$ . Determine the area of the triangle $AEF$.
Let $ABC$ be an equilateral triangle with side 3. A circle $C_1$ is tangent to $AB$ and $AC$.
A circle $C_2$, with a radius smaller than the radius of $C_1$, is tangent to $AB$ and $AC$ as well as externally tangent to $C_1$.
Successively, for $n$ positive integer, the circle $C_{n+1}$, with a radius smaller than the radius of $C_n$, is tangent to $AB$ and $AC$ and is externally tangent to $C_n$.
Determine the possible values for the radius of $C_1$ such that 4 circles from this sequence, but not 5, are contained on the interior of the triangle $ABC$.
Let $ABC$ be an acute triangle inscribed on the circumference $\Gamma$. Let $D$ and $E$ be points on $\Gamma$ such that $AD$ is perpendicular to $BC$ and $AE$ is diameter. Let $F$ be the intersection between $AE$ and $BC$.
Prove that, if $\angle DAC = 2 \angle DAB$, then $DE = CF$.
Let $ABC$ be a triangle and $k < 1$ a positive real number. Let $A_1$, $B_1$, $C_1$ be points on the sides $BC$, $AC$, $AB$ such that$$\frac{A_1B}{BC} = \frac{B_1C}{AC} = \frac{C_1A}{AB} = k.$$
(a) Compute, in terms of $k$, the ratio between the areas of the triangles $A_1B_1C_1$ and $ABC$.
(b) Generally, for each $n \ge 1$, the triangle $A_{n+1}B_{n+1}C_{n+1}$ is built such that $A_{n+1}$, $B_{n+1}$, $C_{n+1}$ are points on the sides $B_nC_n$, $A_nC_n$ e $A_nB_n$ satisfying$$\frac{A_{n+1}B_n}{B_nC_n} = \frac{B_{n+1}C_n}{A_nC_n} = \frac{C_{n+1}A_n}{A_nB_n} = k.$$Compute the values of $k$ such that the sum of the areas of every triangle $A_nB_nC_n$, for $n = 1, 2, 3, \dots$ is equal to $\dfrac{1}{3}$ of the area of $ABC$.
Let $\Theta_1$ and $\Theta_2$ be circumferences with centers $O_1$ and $O_2$, exteriorly tangents. Let $A$ and $B$ be points in $\Theta_1$ and $\Theta_2$, respectively, such that $AB$ is common external tangent to $\Theta_1$ and $\Theta_2$. Let $C$ and $D$ be points on the semiplane determined by $AB$ that does not contain $O_1$ and $O_2$ such that $ABCD$ is a square. If $O$ is the center of this square, compute the possible values for the angle $\angle O_1OO_2$.
On a convex quadrilateral $KLMN$, the side MN is perpendicular to the diagonal $KM$, the side $KL$ is perpendicular to the diagonal $LN$ , $MN=65$ and $KL=28$. The straight through L perpendicular on side $KN$ intersects diagonal $KM$ at $O$, with $KO= 8$. Find the length of the segment $MO$.
In the acute triangle $ABC$, the altitudes $BE$ and $CF$ intersect at $H$, with $E$ on the side $AC$ and $F$ on the side $AB$ . Suppose the circumcenter of $ABC$ lies on segment $EF$. Prove that$$HA^2 = HB^2 + HC^2.$$
Let $ABC$ be a triangle and $AD$, $BE$ and $CF$ their altitudes , with $D, E$ and $F$ on sides $BC$, $CA$ and $AB$, respectively. Suppose orthocenter $H$ is the midpoint of altitude $AD$. Determine the smallest possible value that $$\frac{HB}{HE}+\frac{HC}{HF}$$ can take .
The points $C$ and $D$ lie pn a semicircle of diameter AB as shown in the figure below:
https://cdn.artofproblemsolving.com/attachments/d/0/bace71f90c2299a042197488e2a0f75dbebc37.png
The points $C$ and $D$ can move on a semicircle, such that arc $CD$ is always constant and equal to $70^o$.
a) Explain why line $EF$ is always perpendicular to $AB$.
b) Calculate the angles $AEB$ and $AFB$.
c) Determine the set of points $E$ when the points $C$ and $D$ move along the semicircle.
In a triangle $ABC$ where the angle $\angle BAC$ is equal to $60^o$, choose a point from its interior so that the angles $\angle APB$, $\angle BPC$ and $\angle CPA$ are equal to $120°$. If $AP = a$, find the area of the triangle $BPC$.
source: http://www.omerj.org/









No comments:
Post a Comment