geometry problems from Saint Petersburg State University School Mathematical Olympiad (Russia) with aops links
collected inside aops here
2010-21
year x stands for school year x-1, to x
unknown grade (Juniors - Seniors)
Point $N$ lies on the hypotenuse $AB$ of the right-angled triangle $ABC$. Find its area if $AN = 3, BN = 7$ and $CN = 6$.
Point $M$ lies on the hypotenuse $AB$ of the right-angled triangle $ABC$. Find its area if $AM = 7, BM = 4$ and $CM = 7$.
The base $H$ of the altitude $CH$ of triangle $ABC$ lies on the side $AB$, and $\angle ACH = \angle BCM$, where $CM $ is the median of triangle $ABC$. Find $BC$ if $AB = 10$ and $AC = b$. Indicate the number of solutions depending on $b$.
A circle inscribed in the trapezoid $ABCD$ touches its lateral side $BC$ at point $K$. Find the area of the trapezoid if it is known that $AB = a$, $BK = b$ and $CK =c$.
A circle inscribed in trapezoid $ABCD$ touches its lateral sides $BC$ and $AD$ at points $K$ and $L$, respectively. Find the area of a trapezoid if it is known that $AB = a, BK = b$, and $DL = d$.
The acute angle of a right trapezoid is equal to the angle between the diagonals of the trapezoid and one of the diagonals is perpendicular to one of the lateral sides. Find the ratio of the lengths of the bases of the trapezoid.
In a rectangular trapezoid, the acute angle between the diagonals is equal to $arctg3$ and one of the diagonals is perpendicular to one of the lateral sides. Find the ratio of the lengths of the bases of the trapezoid.
At the base of the pyramid lies a rhombus with side $a$ and an acute angle $\alpha$. Find the volume of a sphere inscribed in a pyramid if each of the dihedral angles at the base is equal to $\beta$.
A convex quadrangle is inscribed in a circle. Find the sum of the products of the opposite sides of the quadrangle if its area is $S$ and the angle between the diagonals is $\alpha$.
Find all values of the parameters $a$ and $b$ such that the intersection points of the parabola $y = x^2-1$ with the axis $Ox$ and the point $(a, b)$ form an obtuse triangle.
The diagonals of the quadrilateral $ABCD$ meet at point $E$. The area of triangle $AEB$ is $6$, the area of triangle $DEC$ is $24$, and the areas of triangles $AED$ and $BEC$ are equal. Find the area of a quadrilateral $ABCD$.
2013.1.21 In triangle $ABC$, point $K$ divides the median $AM$ in the ratio $AK: KM = 1: 2$. Straight line $BK$ meets $AC$ at point $E$. Find $AE$ if $AC = x$
Two isosceles triangles with the same angles at the base equal to $\alpha$ have a common side equal to $a$ (the triangles are connected externally). Find the area of the resulting quadrangle.
Juniors (grades 6-9)
The median $AM$ is drawn in triangle $ABC$. Can the radius of a circle inscribed in triangle $ABM$ be exactly twice the radius of a circle inscribed in triangle $ACM$?
The median $AM$ is drawn in triangle $ABC$. Can the radius of a circle inscribed in triangle $ABC$ be exactly twice the radius of a circle inscribed in triangle $ABM$?
You are given a convex quadrilateral $ABCD$. It is known that $\angle CAD = \angle DBA = 40^o$, $\angle CAB = 60^o$, $\angle CBD = 20^o$,. Find $\angle CDB$.
The diagonals of the rectangle $ABCD$ intersect at point $O$, and on the side $AD$ a point $K$ was chosen such that $AK = 2$, $KD = 1$. It turned out that $\angle ACK = 30^o$. What can be equal to the segment $OK$?
$AM$ is the median of triangle $ABC$. It turned out that the angle $ACB$ is half the angle $CAM$, and the side $AB$ is twice the median $AM$. Find angles of the triangle $ABC$.
In a quadrilateral $ABCD$, where $AB <2AD$, and all angles are right, point $E$ is the midpoint of side $AB$, $F$ is a point on the segment $CE$ such that the angle $CFD$ is equal to $90$ degrees. Prove that triangle $FAD$ is isosceles.
On the side $AB$ of the convex quadrilateral $ABCD$, the square $ABEF$ is constructed so that that the points $C, D, E$ and $F$ lie on the same side of the line $AB$. It is known that $AB =BC$, $AD = DC$ and $\angle ADC = 90^o$. Prove that points $C, D$ and $E$ are collinear.
In right-angled triangle $ABC$, the altitude $AH$ is drawn to the hypotenuse $BC$. In triangles $ABH$ and $ACH$ are inscribed circles with centers $P$ and $Q$, respectively. Prove that $BPQC$ is cyclic.
On the side $AC$ of an isosceles triangle $ABC$ ($AB = AC$) mark a point $D$ such that $BD = BC$. A point $E$ is marked on side $AB$ such that $EB = ED$, and on the extension of the segment $DE$ beyond the point $E$ there is a point $F$ such that $FD = BC$. Point $G$ is the foot of the perpendicular drawn from point $F$ on the side $AB$. It turned out that $GB = GF$. Find the angle $\angle BAC$.
Diagonals of a convex quadrilateral $ABCD$ in which $\angle DAC = \angle BDC = 36^o$, $\angle CBD = 18^o$ and $\angle BAC = 72^o$, intersect at point $P$. Find $\angle APD$
Points $K$ and $L$ are selected on the diagonal $AC$ of rectangle $ABCD$ such that $AK = AB$ and $AL = AD$. Points $M$ and $N$ are the feet of the perpendiculars drawn on the side $AB$ from points $K$ and $L$ respectively. Prove that $AM + LN = AC$.
Points $A$ and $B$ are taken on the circle with center $O$ so that the angle $AOB$ is $60^o$. From an arbitrary point $R$ of small arc $AB$, segments $RX$ and $RY$ are drawn so that point $X$ lies on segment $OA$ and point $Y$ lies on segment $OB$. It turned out that the angle $RXO$ is $65^o$ and the angle $RYO$ is $115^o$ . Prove that the length of segment $XY$ does not depend on the choice of point $R$.
$QL$ is the angle bisector of the triangle $PQR$, and $M$ is the center of the circumscribed circle of a triangle $PQL$. It turned out that the points $M$ and $L$ are symmetric wrt $PQ$. Find the angles of the triangle $PQL$.
Point $K$ is selected on the median $CM$ of triangle $ABC$. Line $AK$ intersects side $BC$ at point $A_1$, and line $BK$ intersects side $AC$ at point $B_1$. It turned out that the quadrilateral $AB_1A_1B$ is cycic. Prove that triangle $ABC$ is isosceles.
The angle bisector $AL$ is drawn in triangle $ABC$. From point $B$ the altitude was drawn on $AL$, that cuts the side $AL$ at point $H$, and the circumcribed circle of triangle $ABL$ at point $K$. Prove that the center of the circumscribed circle of triangle $ABC$ lies on line $AK$.
The sides $AB$ and $AD$ of the cyclic quadrilateral $ABCD$ are equal. On side of $CD$ a point $K$ is chosen such that $\angle DAK = \angle ABD$. Prove that $AK^2 = KD^2 + BC \cdot KD$
Center $O$ of a circle circumscribed around a quadrilateral $ABCD$ lies on the side $AB$ . Point $E$ is symmetrical to $D$ wrt line $AB$. The segments $AC$ and $DO$ intersect at point $P$, and the segments $BD$ and $CE$ at point $Q$. Prove that $PQ$ is parallel to $AB$.
$SM$ is the angle bisector in triangle SQT. Point $O$ on the side $ST$ is such that the angle $OQT$ is equal to the sum of the angles $QTS$ and $QST$ . Prove that $OM$ is the bisector of the angle $QOT$,
Let $RE$ be the bisector of the triangle $RST$. Point $D$ on the side $RS$ is such that $ED \parallel RT$, $F$ is the intersection point of $TD$ and $RE$. Prove that if $SD = RT$ then $TE = TF$
Given a quadrangle $ELMI.$ It is known that the sum of the angles $LME$ and $MEI$ equal to $180$ degrees and $EL = EI + LM$. Prove that the sum of the angles $LEM$ and $EMI$ equal to the angle $MIE$.
Given a parallelogram $ABCD$. The circumscribed circle $\omega$ of triangle $ABC$ intersects side $AD$ and the extension of side $DC$ for the second time at points $P$ and $Q$, respectively. Prove that the center of the circumcircle of a triangle $PDQ$ lies on $\omega$.
Given a parallelogram $ABCD$. From vertex $B$, we draw the perpendicular $BO$ on the side $AD$. Circle $\omega$ centered at point $O$ passes through points $A, B$ and intersects the extension of side $AD$ at point $K$. Segment $BK$ intersects side $CD$ at point $L$, and ray $OL$ intersects the circle $\omega$ at the point $M$. Prove that $KM$ is bisector of angle $BKC$.
Given a parallelogram $ABCD$. A circle touches the side $AC$ of the triangle $ABC$, as well as the extensions of the sides $BA$ and $BC$ at points $P$ and S, respectively. The segment $PS$ meets the sides $DA$ and $DC$ at points $Q$ and $R$. Prove that the incircle of triangle $CDA$ touches sides $AD$ and $DC$ at points $Q$ and $R$.
You are given a parallelogram $ABCD$ with an angle $\angle B$ equal to $60^o$. Point $O$ is the center of the circumscribed circle of triangle $ABC$. Line $BO$ intersects the bisector of the external angle $\angle D$ at point $E$. Find the ratio $BO:OE$.
Trapezoid $ABCD$ ($AB \parallel CD$) is inscribed in a circle $\omega$. On the ray $DC$ beyond the point $C$, point $E$ is marked such that $BC = BE$. Line $BE$ intersects for the second time circle $\omega$ at the point $F$ lying outside the segment $BE$. Prove that the center of the circumcircle of triangle $CEF$ lies on $\omega$.
Let point $O$ in triangle $KIA$ be the foot of the median from the vertex $K, Y$ be the foot of the perpendicular drawn from point $I$ to the bisector of the angle $IOK$, $Z$ be the foot of the perpendicular drawn from point A to the bisector of the angle $AOK$. Let $X$ be the intersection point of the segments $KO$ and $YZ$. Prove that $YX = ZX$.
In the triangle$ BMW $, where $BM <BW <MW$, $BO$ is the altitude , $BH$ is the median. Point $K$ is symmetric to point $M$ wrt point $O$. Perpendicular to $MW,$ drawn through the point $K$ meets the segment $BW$ at the point $ P$. Prove that if $MP$ and $BH$ are perpendicular, then the angle $B$ of the $BMW $triangle is $90$ degrees.
In triangle $KIA$, angles $K$ and $I$ are equal to $30^o.$ On a straight line passing through point $K$ , perpendicular to side $KI$, point $N$ is marked so that $AN$ is equal to $KI$. Find the angle $KAN$
In a convex quadrilateral $FIDO$, opposite sides $FI$ and $DO$ are equal to each other and more than the side $DI$ . It is known that $\angle FIO = \angle DIO$. Prove that $FO$ is greater than $DI$
$KIA$ is an isosceles triangle with base $KA$ and angles at the base $30^o$. Point $R$ bisects side $KI$. Point $Q$ is symmetric to $R$ with respect to the base of the triangle. $P$ is the intersection point of $IQ$ and $KA$. $E$ is the intersection point of lines $PR$ and $IA$. Prove that $RE = IQ$.
In triangle $ABC$, using on the side $BC = 7$ as the diameter, circle $\omega$ is constructed. Side $AB$ is visible from the center $\omega$ at an angle of $60^o$. The median of the triangle drawn from point $A$, intersects $\omega$ at point $D$. Line $CD$ intersects side $AB$ at point $E$. Find the perimeter of triangle $ADE$ if point $D$ is the midpoint of the median.
$KIA$ is an isosceles triangle with base $KA$. On sides $KA$, $AI$ and $IK$, points $M , N$ and $P$ are chosen, respectively, such that the angles $PMK$ and $NMA$ are equal. Through vertex $A$ a line parallel to $PN$ is drawn, $Q$ is the intersection point of this line and segment $MP$ . Prove that $QK = QA$.
Loser Vasya claims that the following criterion for the congruence of triangles is true, the formulation of which he saw in a dream: if triangles $ABC$ and $XY Z$ have equal medians $BM$ and $Y N$ , and also $\angle ABM = \angle XY N$ and $\angle CBM = \angle ZY N$ , then triangles $ABC$ and $XY Z$ are congruent. Excellent student Petya believes that this sign of equality is wrong. Find out which one is right.
When distributing land plots, farmer Novoselov was allocated $2$ square plots of different sizes, with integer sides. Is it possible to allocate to the farmer Malinnikov also $2$ square sections with integer sides, so that the total the area of Malinnikov's plots was $2$ times larger than the total areas of plots Novoselov?
Points $Q$ and $F$ are marked on side $NA$ of triangle $NBA$ such that $NQ = FA = NA/4$. A point $L$ is chosen on the segment $QF$. Straight lines are drawn through the points $Q$ and $F$, parallel to $BL$, until they intersect with sides $NB$ and $AB$ at points $D$ and $K$, respectively. Is it true that the sum of the areas of triangles $NDL$ and $AKL$ is $2$ times less than the area triangle $NBA$?
Vasya, a loser, dreamed that the following statement is true: if in triangle on $ABC$, median $CC_1$ drawn to side $AB$ is greater than median $AA_1$ drawn to side of $BC$, then $\angle CAB$ is less than $\angle BCA$. The excellent student Petya believes that this statement is erroneous. Find out which one is right.
A square of $5 \times 5$ cells was cut into several parts of different areas, each of which consists of a whole number of cells. What is the maximum number of pieces that could be obtained with such a cut?
On side $AC$ of triangle $ABC$, where $\angle ACB = 45^o$, there is a point $K$ such that $AK = 2KC$. A point $S$ was found on the segment $BK$ such that $AS \perp BK$ and $\angle AKS = 60^o$. Prove that $AS = BS$.
Altitudes of an acute-angled non-isosceles triangle $ABC$, drawn from vertices $A$ and $C$ intersect at point $H$ and also intersect the bisector of angle $ABC$ at points $F$ and $G$, respectively. Prove that the triangle $FGH$ is isosceles.
Points $E$ and $F$ are marked on side $BC$ of square $ABCD$ such that $BE : EC = CF : FB = 1 : 2$. A point $G$ is marked on side $CD$ so that $CG : GD = 2 : 1$. Points $H$ and $I$ are marked on side $AD$ such that $AI : ID = DH : HA = 1 : 2$. Segment $BG$ intersects segments $AE$, $IF$ and $HC$ at points $J , K$ and $L$ respectively. Which of the quadrilaterals has the larger area, $EFKJ$ or $GDHL$?
Juniors Finals (grades 6-7)
Points $A B, C, D$ are located on the straight line (in that order). Point $E$ is marked on the plane containing this line. It turned out that $AB = BE$ and $EC = CD$. Prove that the angle $AED$ is obtuse.
You are given an isosceles triangle $ABC$ with base $BC$. Point $M$ is the midpoint of side $AC$, point $P$ is the midpoint of $AM$, point $Q$ is marked on side $AB$ so, that $AQ = 3BQ$. Prove that $BP + MQ> AC$.
Points $D$ and $E$ are taken in an acute-angled triangle $ABC$ on side $AB$ (point D lies on segment $AE$), while $AD = BE$, $DE <AD$. On side $BC$, point $G$ is chosen such that line $EG$ is parallel to the bisector of angle $BAC$. Point $F$ is the foot of the perpendicular drawn on the side $AC$ from point $D$. Prove that $FD + EG> DE$.
An angle $ABC$ of $100^o$ is given. On the plane on opposite sides of the straight line $AB$ are markedpoints $D$ and $E$ such that $BC = CD = AE$, $\angle BCD = 60^o$, $\angle BAE = 160^o$ (point $D$ lies outside angle $ABC$). Prove that the line $DE$ passes through the midpoint of the segment $AB$.
In triangle $ABC$, point $D$ is the midpoint of side $AB$, $E$ is the midpoint of side $AC$, $F$ is the midpoint bisector $AL$, and $DF = 1$, $EF = 2$. Points $D, E, F$ are drawn on the plane so that the line $DF$ horizontal, and the rest of the drawing elements are erased. Is it possible to restore the position of at least one from the vertices of the triangle, if it is known that the vertex $A$ was above the line $DF$ ?
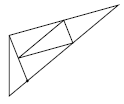
A certain triangle was cut into five small triangles as shown in figure. Could all five small triangles be congruent in this case?
Each variant had a different figure.
Juniors Finals (grades 8-9)
Let $ABC$ be a triangle with angle $\angle C = 60^o$, angle bisectors $AA_1$ and $BB_1$. Prove that $AB_1 + BA_1 = AB$.
Point $O$ is marked on side $AB$ of triangle $ABC$. Circle $\omega$ centered at the point $O$ meets the segments $AO$ and $OB$ at the points $K$ and $L$, respectively, and touches the sides $AC$ and $BC$ at the points $M$ and $N$, respectively. Prove that the intersection point of the segments $KN$ and $LM$ lies at the altitude $CH$ of triangle $ABC$.
A circle $\omega_1$ is circumscribed around the quadrilateral $ABCD$. Across points $A$ and $B$ a circle $\omega_2$ is drawn, intersecting the ray $DB$ at the point $E \ne B$. The ray $CA$ meets the circle $\omega_2$ at the point $F \ne A$. Prove that if the tangent to the circle $\omega_1$ at the point $C$ is parallel to the straight line $AE$, then the tangent to the circle $ \omega_2$ at the point $F$ is parallel to the line $AD$.
The circle $\omega$ is circumscribed around an acute-angled triangle $ABC$. The tangent to the circle $\omega$ at the point $C$ meets the line $AB$ at the point $K$. Point $M$ is the midpoint of segment $CK$. Line $BM$ intersects for the second time circle $\omega$ at point $L$, and line $KL$ intersects the circle for the second time $\omega$ at point $N$. Prove that lines $AN$ and $CK$ are parallel.
Given a triangle $ABC$. On its sides $BC, CA$ and $AB$, the points $A_1, B_1$ and $C_1$ are respectively chosen such that the quadrilateral $AB_1A_1C_1$ is cyclic. Prove that$$\frac{4S_{A_1B_1C_1}}{S_{ABC}}\le \left(\frac{B_1C_1}{AA_1}\right)^2$$
Let $M$ be the intersection point of the medians of the triangle $ABC$. A line passing through $M$ intersects segments $BC$ and $CA$ at points $A_1$ and $B_1$, respectively. Point $K$ is the midpoint of side $AB$. Prove that $9S_{KA_1B_1} \ge 2S_{ABC}$.
Given a trapezoid $ABCD$. On the bases $BC$ and $AD$, points are respectively selected $Q$ and $S$. Segments $AQ$ and $BS$ intersect at point $P$, and segments $CS$ and $DQ$ intersect at point $R$. Prove that $S_{PQRS} \le \frac14 S_{ABCD}$.
The circle $\omega$ is circumscribed around an isosceles triangle $ABC$. The extension of the altitude $BB_1$, drawn on the lateral side $AC$, intersects the circle $\omega$ at point $D$. From point $C$ , the perpendicular $CC_1$ is drawn on the lateral side $AB$ and the perpendicular $CH$ is drawn on straight line $AD$. Prove that $S_{BCB_1C_1}\ge S_{HCC_1}.$
Inside triangle $ABC$, a point $D$ is chosen such that $\angle ABD = \angle ACD$ and $\angle ADB = 90^o$. Points $M$ and $N$ are midpoints of sides $AB$ and $BC$, respectively. naturally. Find the angle $\angle DN M$.
Given an non-isosceles acute-angled triangle $ABC$. On rays $AB$ and $AC$, respectively points $K$ and $L$ such that the quadrangle $KBCL$ is cyclic. Point $H$ is the foot of the sltitude drawn from vertex $A$ on side $BC$. Prove that if $KH = LH$ then $H$ is the center of the circumcircle of the triangle $AKL$.
In an acute-angled triangle $ABC$, heights $BD$ and $CE$ are drawn. Point $X$ is taken inside the triangle. Let $X_1$ be a point symmetric to $X$ wrt line $AB, X_2$ be a point symmetric to $X_1$ wrt line $BC$, and $X_3$ is a point symmetric to $X_2$ wrt line $CA$. Point $M$ is the midpoint of segment $XX_3$. Prove that points $D, E$ and $M$ lie on one straight line.
In an acute-angled triangle $ABC$ with the smallest side $AB$, the altitudes $BB_1$ and $CC_1$ are drawn, they intersect at point $H$. Through point $C_1$ we draw a circle $\omega$ centered at point $H$ and a circle $\omega_1$ with center at point $C$. Through point $A$, draw a tangent to $\omega$ at the point $K$, as well as the tangent line to $\omega_1$ at the point $L$. Find $\angle KB_1L$.
Point $D$ is marked on side $BC$ of triangle $ABC$, and on segment $AD$ such point $E$ such that $\angle CED =\angle ABC$. Point $M$ is the midpoint of segment $BD$, and point $H$ is the foot of the perpendicular drawn from point $A$ on side $BC$. A point $K$ was chosen at the perpendicular bisector of segment$ DE$ , and a point $L$ was chosen on the segment $AH$ such that $DKLM$ parallelogram. Prove that lines $AC$ and $LM$ are perpendicular.
A circle with center $O$ is circumscribed around a quadrilateral $ABCD$ with perpendicular diagonals. Points $P$ and $Q$ are the midpoints of arcs $ABC$ and $ADC$ of this circle. Line $BO$ intersects segment $CQ$ at point $R$. On side $AB$, point $S$ is chosen such that the lines $AQ$ and $RS$ are parallel. Prove that lines $CS$ and $PD$ are perpendicular.
Point $H$ is the orthocenter of triangle $ABC$. On sides $AB$ and $BC$ respectively points $L$ and $N$ are taken such that lines $AH$ and $LN$ are parallel. Point $M$ is the midpoint of the segment $LN$ and lies on the circumcircle of triangle $CHN$. Prove that $ \angle BAM = \angle BCM$.
Point $M$ is the midpoint of side $AB$ of a non-isosceles triangle $ABC$, and point $O$ is the center of a circle around it. Circle with $CM$ diameter intersects for second time the sides $AC$ and $BC$ at points $P$ and $R$, respectively. Point $Q$ is midpoint of line $PR$. Prove that lines $CO$ and $MQ$ are parallel.
In triangle $ABC$, point $D$ is the midpoint of side $AB$, $E$ is the midpoint of side $AC$, $F$ is the midpoint bisector $AL$, and $DF = 1$, $EF = 2$. Points $D, E, F$ are drawn on the plane so that the line $DF$ horizontal, and the rest of the drawing elements are erased. Is it possible to restore the position of at least one from the vertices of the triangle, if it is known that the vertex A was above the line $DF$ ?
A point $K$ is marked on side $BC$ of triangle $ABC$. To the circumscribed circle of the triangle $AKC$, the tangent $\ell_1$ is drawn, parallel to the line $AB$ and nearest to it. It touched circle at point $ L$. Line $AL$ intersects the circumscribed circle of triangle $ABK$ at point $M$ ($M \ne A$). The tangent $\ell_2$ is drawn to this circle at the point $M$. Prove that the lines $BK$, $\ell_1$ and $\ell_2$ intersect at one point.
Circles $\omega_1$ and $\omega_2$ intersect at points $K$ and $L$. Line $\ell$ intersects circle $\omega_1$ at points $A$ and $C$, and the circle $\omega_2$ at points $B$ and $D$, moreover, the points lie on the line $\ell$ in alphabetical order . Denote by $P$ and $Q$, respectively, the projections of the points $B$ and $C$ onto the line $KL$. Prove that lines $AP$ and $DQ$ are parallel.
Points $B_1$ and $C_1$ are the midpoints of sides $AC$ and $AB$ of triangle $ABC$. With sides $AB$ and $AC$ as diameters, circles $\omega_1$ and $\omega_2$ are constructed. Denote by $D$ the point intersection of the line $B_1C_1$ with the circle $\omega_1$, lying on the other side of $C$ with respect to line $AB$. Denote by $E$ the intersection point of line $B_1C_1$ with circle $\omega_2$ lying on the other side of $B$ with respect to line $AC$. Lines $BD$ and $CE$ intersect at point $K$. Prove that line $BC$ passes through the intersection point of altitudes of the triangle $KDE$.
The circle $\omega$ passing through points $B$ and $C$ intersects sides $AB$ and $AC$ of triangle $ABC$ at points $K$ and $L$, respectively ($K \ne B$ and $L \ne C$). A point $P$ is marked on the ray $BL$ such that $BP = AC$, and a point $Q$ is marked on the ray $CK$ such that $CQ = AB$. Prove that the center of the circumscribed circle of triangle $APQ$ lies on $\omega$.
Points $A_1$ and $B_1$ are the midpoints of sides $BC$ and $AC$ of an acute-angled triangle $ABC$, point $M$ is the midpoint of segment $A_1B_1$. Point $H$ is the foot of the altitude drawn from vertex $C$ to side $AB$. Through point $M$, circles are drawn tangent to sides $BC$ and $AC$, respectively, at points $A_1$ and $B_1$. Denote the second intersection point of the circles by $N$. Prove that points $H, M$ and $N$ lie on one straight line.
Diagonals of quadrilateral $ABCD$ intersect at point $O$. Diagonal $AC$ is bisector of angle $\angle BAD$, point $M$ is the midpoint of side $BC$, and point $N$ is the midpoint of segment $DO$. Prove that quadrilateral $ABCD$ is inscribed if and only if quadrilateral $ABMN$ is inscribed.
The circle inscribed in triangle $ABC$ has center $I$ and touches sides $BC$ and $AC$ at points $A_1$ and $B_1$ respectively. The perpendicular bisector of segment $CI$ intersects side $BC$ at point $K$. Through point $I$, a line perpendicular to $KB_1$ is drawn, it intersects side $AC$ at point $L$. Prove that lines $AC$ and $A_1L$ are perpendicular.
Seniors Qualifying (grades 10-11)
Altitudes $AA_1, BB_1, CC_1$ are drawn in an acute-angled triangle $ABC$. Let $CC_2$ be the atlitude of the triangle $CA_1B_1 $, $BB_2$ be the atlitude of the triangle $BA_1C_1$. Prove that $C_1B_2 = B_1C_2$.
Points $M$ and $G$ are marked on side $BC$ of convex quadrilateral $ABCD$ (point $M$ lies between $B$ and $G$) so that the angle $BAM$ is equal to the angle $CDG$ and the angle $MAG$ is equal to angle $MDG$ . Prove that the angle $CAG$ is equal to the angle $BDM$.
The angle bisector $QK$ of the triangle $PQR$ intersects it's circumcircle at point $M$ (other than $Q$). The circumscribed circle of the triangle $PKM$ meets the extension of the side $PQ$ beyond the point $P$ at the point $N$. Prove that $NR$ and $QM$ are perpendicular.
A circle with center $O$ inscribed in angle $QPR$, touches the side $PR$ at point $L$. The tangent to the circle, parallel to $PO$, intersects ray $PQ$ at point $S$, and ray $LP$ at point $D$. Prove that $DS = 2PL$.
Circles $K_1$ and $K_2$ are tangent to one straight line at points $A$ and $B$, respectively, and, moreover, they intersect at points $X$ and $Y$, of which point $X$ lies closer to line $AB$. Line $AX$ intersects $K_2$ for the second time at point $P$. The tangent line to $K_2$ at point $P$ meets line $AB$ at point $Q$. Prove that the angle $XYB$ is equal to $BYQ$.
The diagonals of the trapezoid $RSQT$ with the bases RS and QT intersect at point $A$ at right angles. The base $RS$ is known to be larger than the $QT$ base and the angle $R$ is right. The bisector of the angle $RAT$ intersects $RT$ at the point $U$, and the line, passing through point $U$ parallel to $RS$, intersects line $SQ$ at point $W$. Prove that $UW = RT$
In a triangle $XYZ$, the side $YZ$ is twice the size of the side $XZ$. A point $W$ is selected on the side $YZ$ so that the angles $ZXW$ and $ZYX$ are equal. Line $XW$ intersects the bisector of the outer angle at the vertex $Z$ at point $A$. Prove that angle $YAZ$ is right.
In a $KIA$ triangle, the side $KA$ is smaller than the side $KI $, and the points $R$ and $E$ are the feet of the perpendiculars drawn on the bisector of the angle $K$ from the points $I$ and $A$ respectively. Prove that the lines $IE, RA$ and the perpendicular to$ KR$, drawn at point $K$, intersect at one point.
The midpoints of the sides $BA, AN, NB$ of the triangle $NBA$ are denoted by points $L$, E and $D$, respectively, and the intersection point of the angle bisectors of the triangle $NBA$ is $X$. Let $P$ be the point of intersection of lines $BX$ and $EL$, $V$ be the point of intersection of lines $AX$ and $DL$, $T$ and $S$ be the points where line $PV$ meets sides $NB$ and $NA$, respectively. Prove that the triangle $NTS$ is isosceles.
In triangle $KIA$, whose side $KI$ is less than the side $KA$, the bisector of angle $K$ intersects side $IA$ at point $O$. Let $N$ be the midpoint of $IA$, and $H$ is the foot of the altitude drawn from point $I$ on the segment $KO$. Line $IH$ intersects segment $KN$ at point $Q$. Prove that $OQ$ and $KI$ are parallel.
The altitude $AK$ is drawn in an acute-angled triangle $SAP$. On the side $PA$ chose point $L$, and on the extension of side $SA$ beyond point $A$ chose point $M$ such that $\angle LSP = \angle LPS$ and $\angle MSP = \angle MPS$. Lines $SL$ and $PM$ intersect line $AK$ at points $N$ and $O$, respectively. Prove that $2ML = NO$.
In the triangle $KOI$, on the side $KO$ , point M is marked so that $KM = MI$, and on the side $IO$ , point $S$ is marked so that $SI = SO$. Point $U$ is marked on line $KS$ so that line $MU$ is parallel to line $KI$. Prove that the angle $KOI$ is equal to angle $MIU$ .
$SPBU$ is a convex quadrilateral, $O$ is the point of intersection of its diagonals. It turned out that the angles $OSP$, $SOP$ and $BU O$ are equal to $30^o$. $N$ is the midpoint of $SU$. A straight line drawn through $N$ perpendicular on $SU$ , intersects the extension of the median of the triangle $POB$, drawn from the vertex $O$, at the point $A$. Find the angle $SAU$ .
In a convex quadrilateral $UEFA$, the angle $E$ is half the angle $U$, and on the side $UE$ a point $K$ is marked such that $FK$ is the bisector of angle $F$ and angle $UKA$ is equal to angle $KFE$. Is it true that $EK= KU + U A$?
In triangle $KIA$, the angle $A$ is half the angle $K$. Let $IQ$ be the median of the triangle $KIA$, $AW$ is angle bisector of triangle $QIA$. Prove that the angle $QWA$ is less than $45$ degrees.
Altitudes $AD$ and $CE$ are drawn in an acute-angled triangle $ABC$. From point $D$ is drawn perpendicular $DF$ on side $AB$, and from point $E$ perpendicular $EG$ to side $BC$. Find the ratio of the segments $FE: GD$ if $AE = 4, CD = 5$.
In the triangle $KIA$ on the side $KI$ mark a point $V$ such that $KI = V A$. Then inside the triangle mark a point $X$ such that the angle $XKI$ is equal to half of angle $AV I$, and angle $XIK$ is equal to half of angle $KV A$. Let $O$ be the intersection point of line $AX$ with side $KI$. Is it true that $KO = V I$?
In triangle $ABC$ with sides $AB = 5$, $BC = 6$ and $AC = 4$, $AA_1$ is bisector of angle $\angle BAC$. Further, in triangle $AA_1C$, the bisector $A_1C_1$ of angle $\angle AA_1C$ is drawn, in triangle $C_1A_1C$ the bisector $C_1A_2$ of angle $\angle A_1C_1C$ is drawn, in triangle $C_1A_2C$, the bisector $A_2C_2$ of angle $\angle C_1A_2C$, $...$, in triangle $C_{2020}A_{2020}C$ the bisector $C_{2020}A_{2021}$ of angle $\angle A_{2020}C_{2020}C$ is drawn, in triangle $C_{2020}A_{2021}C$ the bisector $A_{2021}C_{2021}$ of angle $\angle C_{2020}A_{2021}C$ is drawn. Prove that triangles $ABC$ and $A_{2021}C_{2021}C$ are similar and find the ratio of similarity of these triangles.
Point $M$ is the midpoint of the hypotenuse $AC$ of right triangle $ABC$. Points $P$ and $Q$ lie on lines $AB$ and $BC$ respectively such that $AP = PM$ and $CQ = QM$. Find the angle $\angle PQM$ if $\angle BAC = 17^o$.
On the extension of side $AB$ of parallelogram $ABCD$ beyond point $B$ , the point $K$ is marked, and the point $L $is marked on the extension of the side $AD$ beyond the point $D$. It turned out that $BK = DL$. Segments $BL$ and $DK$ intersect at point $M$ . Prove that $CM$ is the bisector of angle $\angle BCD$.
On the side $AC$ of the triangle ABC, as the diameter, a circle is constructed with center $O$ intersecting side $BC$ of this triangle at point $D$. Find the radius of the incircle of triangle ABC, if $OD = 4$, $DC = 3$, and the center of the circumscribed circle of triangle $ABC$ lies on $BO$.
Seniors Finals (grades 10-11) plane geometry
Inside triangle $ABC$ ($AB <BC$) there is a point $O$ equidistant from its three vertices. $BD$ is the bisector of angle $B$. Point $M$ is the midpoint of side $AC$, and point $P$ on ray$ MO$ is such that $\angle APC = \angle ABC$. Point $N$ is the foot of the perpendicular drawn from $P$ on $BC$. Prove that each of the diagonals of the quadrilateral $BDMN$ divides the triangle $ABC$ into two equal parts.
In an acute-angled triangle $ABC$, the side $AB$ is equal to $c$, and the radius of the circumscribed circle is is equal to $R$. The bisectors $AA_1$ and $BB_1$ divide opposite sides in the ratio $m_1:n_1$ and $m_2: n_2$, respectively, counting from the vertex $C$. Find the radius of the circle passing through the center of the circle inscribed in triangle $ABC$, and through points $A_1$ and $B_1$
In a triangle with integer sides, one of the medians is $16$ and the other is $29$. Find the sides of the triangle.
In an isosceles triangle $ABC$ with the base $BC$, points $B_1$ and $C_1$ are the midpoints of the sides $AC$ and $AB$ respectively. Circles circumscribed around triangles $ABB_1$ and $AC_1C$ intersect at points $A$ and $P$. Line $AP$ intersects, the circle circumscribed around the triangle $AC_1B_1$, at points $A$ and $P_1$. Find the ratio $AP_1: AP$.
The diagonals of the cyclic quadrilateral $ABCD$ meet at point $P$. The centers of the circles, cirumscribed around triangles $APB$ and $CPD$, lie on the circle cirumscribed around $ABCD$. Find the angle between lines $AC$ and $BD$.
The diagonals of the quadrangle $ABCD$ are equal and intersect at point $O$. It is known that $\angle AOB = 60^o$, $AB = DO$, $DC = BO$. Find the angles of the quadrilateral.
Two lines perpendicular on $AB$, intersect it at points $M$ and $N$ such that $AM = BN$. Points $X$ and $Y$ are chosen on these straight lines so that the sum of angles $AXB$ and $AYB$ is $180^o$. Find the sum of the angles $ABX$ and $ABY$.
Different points $P$ and $Q$ are marked on the side $AC$ of triangle $ABC$. It is known that $\angle ABP = \angle PBQ$ and $AC \cdot PQ = AP \cdot QC$. Find $\angle PBC$.
Given triangle $ABC$. Line $BC$ intersects with the bisector of the external angle $A$ at point $P$. On the side $BC$ , a point $Q$ is chosen such that $PC \cdot QB = PB \cdot QC$. Find $\angle PAQ$.
Given an isosceles triangle $ABC$ with base $AB$. Point $M$ is the midpoint of side $AC$ of triangle $ABC$, $CH$ is the altitude of $ABC$. The circumcircle of triangle $BCM$ meets $CH$ at point $K$. Find the radius of the circumcircle of triangle $ABC$, if it is known that $CK = 1$.
The diagonals of a convex quadrilateral $ABCD$ intersect at point $O$. It is known that $AB = BC = CD$, $AO = DO$ and $AC\ne BD$. What is the sum $\angle BAD + \angle ADC$?
You are given a convex quadrilateral $ABCD$, in which $AB = AD$ and $CB = CD$. The bisector of angle $BDC$ intersects side $BC$ at point $L$, and segment $AL$ intersects diagonal $BD$ at point $M$. It turned out that $BL = BM$. What is the sum $2 \angle BAD + 3 \angle BCD$?
In a convex quadrilateral $ABCD$, sides $CB$ and $CD$ are equal. The bisector of angle $BDC$ intersects side $BC$ at point$ L$, and segment $AL$ intersects diagonal $BD$ at point $M$. It turned out that $BM = ML$ and $\angle CML = \angle BAD$. What is the sum $4 \angle BAD + 3 \angle BCD$?
Point $H$ is the foot of the altitude drawn from the vertex $A$ of an acute-angled triangle $ABC$. On segment $AH$ a point $K$ is taken such that $\frac{AK}{CH}= \frac{KH}{HB}$. Point $L$ is the foot of the altitude drawn from point $H$ on $BK$. Find the angle $ALC$ .
Point $M$ is the midpoint of the base $BC$ of isosceles triangle $ABC$, and point $L$ is the midpoint of segment $AM$. In triangle $BLM$, altitude $MH$ is drawn. Find the angle $AHC$.
On the side $AC$ of the triangle $ABC$, points $P$ and $Q$ are selected so that $AP = QC <\frac{AC}{2}$. It turned out that $AB^2 + BC^2 = AQ^2 + QC^2$. Find the angle $PBQ$.
On the diagonal $BD$ of the square $ABCD$, point $P$ is selected, and on the side of $CD$, point $Q$ is selected so that the angle $\angle APQ$ is right. Line $AP$ intersects side $BC$ at point $R$. Point $S$ is selected on segment $PQ$ so that $AS = QR$. Find the angle $QSR$.
Inside the circle $\omega$ there are circles $\omega_1$ and $\omega_2$ intersecting at points $K$ and $L$ and tangent to the circle $\omega$ at points $M$ and $N$. It turned out that points $K, M$ and $N$ lie on one straight line. Find the radius of the circle $\omega$ if the radii of the circles $\omega_1$ and $\omega_2$ are $3$ and $5$, respectively.
Inside the circle $\omega$ there is a circle $\omega_1$ tangent to it at the point $K$.The circle $\omega_2$ touches the circle $\omega_1$ at the point $L$ and intersects with the circle $\omega$ at the points $M$ and $N$. It turned out that the points $K, L$ and $M$ lie on one straight line. Find the radius of the circle $\omega$ , the radii of the circles $\omega_1$ and $\omega_2$ itself are $4$ and $7$, respectively.
An isosceles trapezoid $ABCD$ with bases $AB$ and $DC$ is inscribed with a circle centered at point $O$. Find the area of the trapezoid if $OB = b$ and $OC = c$.
Points $K, L$ and $M$ are the midpoints of sides $AB, BC$ and $CD$ of parallelogram $ABCD$. It turned out that the quadrangles $KBLM$ and $BCDK$ are cyclic. Find the ratio $AC: AD$.
Inside triangle $ABC$, a point $P$ is chosen such that $AP = BP$ and $CP = AC$. Find $\angle CBP$ if you know that $\angle BAC = 2\angle ABC$.
Given a triangle $ABC$ with the largest side $BC$. The bisector of its angle $C$ meets the altitudes $AA_1$ and $BB_1$ at points $P$ and $Q$, respectively, and the circle circumscribed around $ABC$ at point $L$. Find $\angle ACB$ if it is known that $AP = LQ$.
On the sides $AB$ and $BC$ of an equilateral triangle $ABC$, points $P$ and $Q$ are chosen such that $AP:PB = BQ:QC = 2:1$. Find $\angle AKB$, if $K$ is the intersection point of the segments $AQ$ and $CP$.
On the hypotenuse $AB$ of an isosceles right-angled triangle $ABC$ such $K$ and $L$ are marked, such that $AK: KL: LB = 1: 2: \sqrt3$. Find $\angle KCL$.
Given a right triangle $ABC$. On the extension of the hypotenuse $BC$, point $D$ is chosen so that line $AD$ is tangent to the circumcircle $\omega$ of triangle $ABC$. Line $AC$ intersects the circumcircle of triangle $ABD$ at point $E$. It turned out that the bisector of $\angle ADE$ touches the circle $\omega$. In what ratio does point $C$ divide $AE$ ?
On the extension of the side $BC$ of triangle $ABC$ is taken, and point $D$ is taken so that line $AD$ is tangent to the circumscribed circle $\omega$ of triangle $ABC$. Line $AC$ intersects the circumscribed circle of triangle $ABD$ at point $E$, and $AC: CE = 1: 2$. It turned out that the bisector of the angle $ADE$ touches the circle $\omega$. Find the angles of triangle $ABC$
A point $D$ is marked on altitude $BH$ of triangle $ABC$. Line $AD$ intersects side $BC$ at point $E$, line $CD$ intersects side $AB$ at point $F$. Points $G$ and $J$ are projections of points $F$ and $E$ on side $AC$, respectively. The area of the triangle $HEJ$ is twice the area of the triangle $HFG$.In what ratio does the altitude $BH$ divide $FE$?
At the altitude $BH$ of triangle $ABC$, some point $D$ is marked. Line $AD$ intersects side $BC$ at point $E$, line $CD$ intersects side $AB$ at point $F$. It is known that $BH$ divides the segment $FE$ in the ratio $1: 3$, counting from point $F$. Find the ratio $FH: HE$.
Given an acute-angled triangle $ABC$ with an angle $\angle ABC = a$. On the extension of side $BC$, a point $D$ is taken such that line $AD$ is tangent to the circumcircle $\omega$ of triangle $ABC$. Line $AC$ intersects the circumcircle of triangle $ABD$ at point $E$. It turned out that the bisector $\angle ADE$ touches the circle $\omega$ . In what ratio does point $C$ divide $AE$?
A triangle $ABC$ with an angle $\angle ABC = 135^o$ is inscribed in a circle $\omega$. Lines tangent to $\omega$ at points $A$ and $C$ meet at point $D$. Find $\angle ABD$ if it is known that $AB$ divides the segment $CD$ in half.
A circle with center $O$ of radius $ r$, touches the sides $BA$ and $BC$ of an acute triangle $ABC$ at points $M$ and $N$, respectively. The straight line passing through the point $M$ parallel to $BC$, intersects the ray $BO$ at the point $K$. On the ray $MN$, the point $T$ is chosen so that $\angle MTK =\frac 12 \angle ABC$. Find the length of $BO$ segment if $KT = a$.
Circle $\omega$ with center $O$ touches sides $BA$ and $BC$ of acute triangle $ABC$ at points $M$ and $N$, respectively. A straight line passing through point $M$ parallel to $BC$ intersects ray $BO$ at point $K$. Point $T$ is chosen on ray $MN$ so that $\angle MTK= \angle ABC$. It turned out that straight $CT$ touches $\omega$ . Find the area of the triangle $OKT$ if $BM = a$.
The median $AM$ is drawn in triangle $ABC$. Circle $\omega$ passes through point $A$, touches line $BC$ at point $M$ and intersects sides $AB$ and $AC$ at points $D$ and $E$, respectively. On the arc $AD$, which does not contain point $E$, a point $F$ was chosen such that $\angle BFE = 72 ^o$. It turned out that $\angle DEF = \angle ABC$. Find $\angle CME$ .
A circle $\omega$ is circumscribed around triangle $ABC$. The straight line tangent to $\omega$ at point $C$ intersects ray $BA$ at point $P$. On ray $PC$, behind point $C$, we have marked a point $Q$ such that $PC = QC$. The segment $BQ$ intersects the circle w at the point $K$ for the second time. On the smaller arc $BK$ of the circle $\omega$, a point $L$ is marked such that $\angle LAK = \angle CQB$. Find the angle $\angle PCA$ if it is known that $\angle ALQ = 60^o$.
Using the segment $AB$ of length $10$ as the diameter, a circle $\omega$ is constructed. A tangent to $\omega$ is drawn through point $A$, at which point $K$ is selected. Through point $K$, a straight line is drawn, different from $AK$, tangent to circle $\omega$ at point $C$. Altitude $CH$ of triangle $ABC$ intersects segment $BK$ at point $L$. Find the area of triangle $CKL$, if known, that $BH: AH = 1: 4$.
Given a right-angled triangle $ABC$ with right angle $C$. On its leg $BC$ of length $26$, a circle is built on its side $BC$. A tangent $AP$ is drawn from point $A$ to this circle, different from $AC$. The perpendicular $PH$ dropped to the segment $BC$ intersects the segment $AB$ at the point $Q$. Find the area of the triangle $BPQ$ if it is known that $BH: CH = 4: 9$.
A circle $\omega$ of radius $r$ is inscribed in triangle $ABC$, which touches side $AB$ at point $X$. Point $Y$ is marked on the circle, diametrically opposite to point $X$. Line $CY$ intersects side $AB$ at point $Z$. Find the area of triangle $ABC$ if it is known that $CA + AZ = 1$.
In a right-angled triangle $ABC$, the altitude $BH$ is drawn on the hypotenuse $AC$. Points $X$ and $Y$ are the centers of circles inscribed in triangles $ABH$ and $CBH$, respectively. Line $XY$ intersects legs $AB$ and $BC$ at points $P$ and $Q$. Find the area of triangle $BPQ$, if you know that $BH = h$.
The angle bisector $AL$ and median $BM$ of triangle $ABC$ meet at point $X$. Line $CX$ meets side $AB$ at point $Y$. Find the area of triangle $CYL$ if it is known that $\angle BAC = 60^o$ and $AL = x$.
In a right-angled triangle $ABC$ with a right angle $B$, the angle bisector $BL$ and the median $CM$ are drawn, they intersect at point $D$. Line $AD$ intersects side $BC$ at point $E$. Find the area of triangle $AEL$ if it is known that $EL = x$.
A perpendicular bisector is drawn to the lateral side $AC$ of an isosceles triangle $ABC$. It intersects the lateral side $AB$ at point $L$, and the extension of the base at point $K$. It turned out that the areas of triangles $ALC$ and $KBL$ are equal. Find the angles of the triangle.
The alitude $AH$ is drawn on the base $BC$ of an isosceles triangle $ABC$. A point $P$ is marked on side $AB$ such that $CP = BC$. The segment $CP$ intersects the height $AH$ at point $Q$. It turned out that the area of triangle $BHQ$ is $4$ times less than the area of triangle $APQ$. Find the angles of triangle $ABC$.
Inside the angle of $30^o$ with vertex $A$, point $K$ is selected, the distances from which to the sides of the angle are equal to $1$ and $2$. Through point $K$, all possible straight lines are drawn that intersect the sides of the angle. Find the minimum rimeter of a triangle cut by a straight line from the angle.
Inside the angle of $30^o$ with vertex $A$, point $K$ is selected, the distances from which to the sides of the angle are equal to $1$ and $2$. Through point $K$, all possible straight lines are drawn that intersect the sides of the angle. Find the minimum area of a triangle cut by a straight line from the angle.
The quadrilateral $ABCD$ is inscribed in a circle. At point $C$, tangent $\ell$ is drawn to this circle. Circle $\omega$ passes through points $A$ and $B$ and touches line $\ell$ at point $P$. Line $PB$ intersects $CD$ at point $Q$. Find the ratio $BC:CQ$ if it is known that $BD$ is tangent to circle $\omega$.
A circle is circumscribed around the triangle $ABC$. The tangents to the circle, drawn at points $A$ and $B$, intersect at point $K$. Point $M$ is the midpoint of the side $AC$. A straight line passing through point $K$ parallel to $AC$, intersects the side $BC$ at point $L$. Find the angle $AML$.
The quadrilateral $ABCD$ is inscribed in a circle $\omega$, the center of which lies on side $AB$. Circle $\omega_1$ touches externally the circle $\omega$ at point $C$. Circle $\omega_2$ touches the circles $\omega$ and $\omega_1$ at points $D$ and $E$, respectively. Line $BC$ intersects the circle $\omega_1$ for second time at point $P$, and line $AD$ intersects circle $\omega_2$ for second time at point $Q$. It is known that points $P, Q$ and $E$ are different. Find the angle $PEQ$.
The quadrilateral ABCD is inscribed in a circle $\omega$, the center of which lies on the side $AB$. Circle $\omega_1$ touchesexternally the circle $\omega$ at point $C$. Circle $\omega_2$ touches the circles $\omega$ and $\omega_1$ at points $D$ and $E$, respectively. Line $BD$ intersects circle $\omega_2$ for second time at point $P$, and line $AC$ secondly intersects circle $\omega_1$ at point $Q$. Find angle $PEQ$.
You are given an acute-angled triangle $ABC$. The circle with diameter $BC$ meets sides $AB$ and $AC$ at points D and $E$, respectively. The tangents drawn to the circle at points $D$ and $E$ meet at point $K$. Find the angle between lines $AK$ and $BC$.
Point $M$ is the midpoint of side $AB$ of triangle $ABC$. Through points $A$ and $M$ a circle $\omega_1$ is drawn tangent to line $AC$, and through points $B$ and $M$ a circle $\omega_2$ is drawn tangent to line $BC$. The circles $\omega_1$ and $\omega_2$ intersect for second time at point $D$. Point $E$ lies inside triangle $ABC$ and is symmetric to point $D$ wrt line $AB$. Find the angle $CEM$.
The circle $\omega$ is circumscribed around triangle $ABC$. Circle $\omega_1$ touches line $AB$ at point $A$ and passes through point $C$, and circle $\omega_2$ touches line $AC$ at point $A$ and passes through point $B$. At point $A$, a tangent is drawn to circle $\omega$, which intersects circle $\omega_1$ for second time at point $X$ and intersects circle $\omega_2$ for second time at point $Y$. Find the ratio $\frac{AX}{XY}$
Around triangle $ABC$, a circle $\omega$ is circumscribed with center at point $O$. Circle $\omega_1$ touches line $AB$ at point $A$ and passes through point $C$, and circle $\omega_2$ touches line $AC$ at point $A$ and passes through point $B$. Through point $A$, a line is drawn that intersects circle $\omega_1$ for second time at point $X$ and circle $\omega_2$ for second time at point $Y$. Point $M$ is the midpoint of segment $XY$. Find the angle $OMX$.
Point $O$ is the center of the circumscribed circle of triangle $ABC$. Point $X$ is selected on the circumscribed circle of triangle $BOC$ outside triangle $ABC$. On rays $XB$ and $XC$, behind points $B$ and $C$, points $Y$ and $Z$ are selected, respectively, such that $XY = XZ$. The circumscribed circle of triangle $ABY$ intersects side AC at point $T$. Find the angle $YTZ$.
Point $O$ is the center of the circumscribed circle of triangle $ABC$. Points $Q$ and $R$ are selected on sides $AB$ and $BC$, respectively. Line $QR$ intersects for second time the circumcircle of triangle $ABR$ at point $P$ and intersects for second time the circumcircle of triangle $BCQ$ at point $S$. Lines $AP$ and $CS$ meet at point $K$. Find the angle between lines $KO$ and $QR$.
Given a triangle $ABC$ with a smaller side $AB$. Points $X$ and $Y$ are chosen on sides $AB$ and $AC$, respectively, so that $BX = CY$. At what angle does the straight line passing through the centers of the circumscribed circles of triangles $ABC$ and $AXY$ intersect the straight line $BC$ and $\angle ABC = \beta$ and $\angle BCA = \gamma$?
Circle $\omega$ of unit radius passes through the vertices $B$ and $C$ of triangle $ABC$ and intersects its sides $AB$ and $AC$ for the second time at points $K$ and $L$, respectively. Points $P$ and $Q$ are marked on rays $BL$ and $CK$, respectively, such that $BP = AC$ and $CQ$ = $AB$. Find the distance between the centers of the circumscribed circles of triangles $APQ$ and $KBC$.
Given an acute angle $BAD$, where point $D$ is different from $A$. On ray $AB$, point $X$ is arbitrarily chosen, also different from $A$. Let $P$ be the point of intersection of the tangents to the circumscribed circle of triangle $ADX$ drawn at points $D$ and $X$. Find the locus of points $P$.
Given an obtuse angle $BAD$, where point $D$ is different from A. On ray $AB$, point $X$ is arbitrarily chosen, also different from $A$. Let P be the point of intersection of the tangents to the circumscribed circle of triangle $ADX$ drawn at points $D$ and $X$. Find the locus of points $P$.
Points $D$ and $X$ are chosen on the sides $BC$ and $AB$ of an acute-angled triangle $ABC$. Lines passing through $X$ parallel to $BC$ and $AD$ intersect the sides AC and BC at the points $Y$ and $Z$, respectively. Let $M, K$ and $N$ be the midpoints of segments $BC, YZ$ and $AD$ respectively. Find the angle $MKN$.
On the side $BC$ of an acute-angled triangle $ABC$, point $D$ is selected, and on the extension of side $AB$ beyond point $B$ point $X$. Lines passing through $X$ parallel to $BC$ and $AD$ intersect rays $AC$ and $CB$, respectively, at points $Y$ and $Z$. Let $M, K$ and $N$ be the midpoints of segments $BC, YZ$ and $AD$, respectively. Find the angle $KMN$.
Given an acute-angled triangle $ABC$. A rectangle $KLMN$ is inscribed in it so that points $M$ and $N$ lie on sides $AB$ and $AC$, respectively, and points $K$ and $L$ lie on side $BC$. Let $AD$ be the median of triangle $ABC$, $E$ be the midpoint of its altitude drawn from the vertex $A$, $O$ be the point of intersection of the diagonals of the rectangle. Find the angle $DOE$.
You are given an acute-angled triangle $ABC$. The rectangle $KLMN$ has vertices $M$ and $N$, respectively, on the extensions of sides $AB$ and $AC$ beyond the point $A$, $K$ and $L$ on side $BC$. Let $AD$ be the median of triangle $ABC$, $B$ be the midpoint of its altitude dtawn from the vertex $A$, $O$ be the intersection point of the diagonals of the rectangle. Find the angle $DBO$.
You are given a quadrilateral $ABCD$ other than a parallelogram. On sides $AB, BC, CD$ and $DA$, points $K, L, M$ and $N$ are selected, respectively, so that $KL\parallel MN\parallel AC$ and $LM \parallel KN\parallel BD$. Find the locus of the intersection points of the diagonals of the parallelogram $KLMN$ .
Given a quadrilateral $ABCD$ other than a parallelogram. On rays $AB, CB,CD$ and $AD$ outside the sides of the quadrilateral $ABCD$, the points $K, L, M$ and $N$ are selected, respectively, so that $KL \parallel MN \parallel AC$ and $LM \parallel KN \parallel BD$. Find the locus of the intersection points of the diagonals of the parallelogram .
A point $P$ is marked on the diagonal $BD$ of parallelogram $ABCD$, which does not lie on the diagonal $AC$. On the ray $AP$, a point $Q$ is taken such that $AP = PQ$. A straight line drawn through point $Q$, parallel to side $AB$, it crossed the side $BC$ at point $R$. Then, through point $Q$, a straight line drawn parallel to side $AD$, crossed line $CD$ at point $S$. Find the angle $PRS$
Points $P$ and $Q$ are marked on the sides $BC$ and $CD$ of parallelogram $ABCD$, respectively, such that $BP = DQ$. Lines $BQ$ and $DP$ intersect at point $M$. Compare angles $BAM$ and $DAM$.
On side $AB$ of triangle $ABC$, a point $P$ is chosen such that $3AP = AB$. In triangles $APC$ and $BPC$, angle bisectors $PK$ and $PL$ are drawn, respectively, and in triangles $APK$ and $BPL$ the altitudes $AQ$ and $BR$ are drawn. In what ratio does line $CP$ divide the segment $QR$?
A point $E$ is taken inside the parallelogram $ABCD$ such that $AE = BC$. Points $M$ and $N$ are the midpoints of segments $AB$ and $CE$, respectively. Find the angle between lines $DE$ and $MN$.
Outside parallelogram $ABCD$, a point $M$ is chosen such that $\angle BAM = \angle BCM$. Points $D$ and $M$ are on opposite sides of lines $AB$ and $BC$. Compare angles $AMB$ and $CMD$.
In parallelogram $ABCD$, side $AB$ is equal to diagonal $AC$. The bisector of ange $CAD$ intersects $CD$ at $P$, and $AC$ and $BP$ meet at $Q$. Find angle $BCD$ if you know $AQ = BQ$.
Inside the parallelogram $ABCD$, on the perpendicular bisector of the side $BC$ , a point $E$ is taken such that $\angle EDC = \angle EBC = a$. Find the angle $AED$.
In parallelogram $ABCD$, the bisector of angle $BAD$ intersects side $CD$ at point $P$, and the bisector of angle $ABC$ intersects diagonal $AC$ at point $Q$. Find the angle between lines $PQ$ and $BD$ if $\angle BPD = 90^o$.
Given a parallelogram $ABCD$ with an acute angle $B$. Outside the parallelogram, a point $K$ is chosen such that the quadrilateral $ABCK$ is inscribed in a circle. Let $L$ be the intersection point of the segments $BK$ and $CD$, $O$ the center of the circumscribed circle of the triangle $DKL$. Find the angle $BCO$.
Point $K$ is chosen inside the triangle $ABC$ on the perpendicular bisector of the side $AB$. The triangles $ABC$ and $BMC$, similar to the triangle $AKB$, are built on the sides $AC$ and $BC$ to the outside. In what respect does the line $LM$ divide the segment$ CK$?
Given an isosceles triangle $ABC$ with base $BC$. On the extension of side $AC$ beyond point $C$, the point $K$ is marked, and the triangle $ABK$ has an inscribed circle with centered at point $I$. A circle is drawn through the points $B$ and $I$ tangent to the line $AB$ at the point $B$. This circle intersects segment $BK$ for the second time at point $L$. Find the angle between the lines $IK$ and $CL$.
An isosceles acute-angled triangle $ABC$ is given. Altitudes $BB_1$ and $CC_1$ are drawn in it , intersecting at the point $H$. Circles $\omega_1$ and $\omega_2$ with centers $H$ and $C$, respectively touch the line $AB$. Tangents, other than $AB$, are drawn from the point $A$ on $\omega_1$ and $\omega_2$. Denote their touchpoints with these circles through $D $ and $E$ respectively. Find the angle $B_1DE$.
Circles $\omega_1$ and $\omega_2$ intersect at points $A$ and $B$, and the circle with center at point $O$ covers circles $\omega_1$ and $\omega_2$ , touching them at points $C$ and $D$ respectively. It turned out, that the points $A, C$ and $D$ lie on the same straight line. Find the angle $ABO$.
A circle is circumscribed around an acute-angled triangle $ABC$. Point $K$ is the midpoint of the smaller arc $AC$ of this circle, and point $L$ is the midpoint of the smaller arc $AK$ of this circle. Segments $BK$ and $AC$ intersect at point $P$. Find the angle between lines $BC$ and $LP$, if it is necessary that $BK = BC$.
The circles $\omega_1$ and $\omega_2$ intersect at points $A$ and $B$, and the circle with center at the point $O$ encloses the circles $\omega_1$ and $\omega_2$, touching them at point $C$ and $D$, respectively. It turned out that points $A, C$ and $D$ lie on the same straight line. Find angle $ABO$.
The circle $\omega_1$ with center $O$ intersects at the points $K$ and $L$ with circle $\omega_2$ , that passing through the point $O$. A line is drawn through the point $O$, intersecting the circle $\omega_2$ for the second time at the point $A$. The segment $OA$ intersects the circle $\omega_1$ at the point $B$. Find the ratio of the distances from point $B$ to lines $AL$ to $KL$.
Circles $\omega_1$ and $\omega_2$ with centers $O_1$ and $O_2$ respectively intersect at point $A$. Line segment $O_2A$ intersects circle $\omega_1$ for the second time at point $L$. The line passing through the point $A$ parallel to $KL$, intersects circles $\omega_1$ and $\omega_2$ for the second time at points $C$ and $D$ respectively. Segments $CK$ and $DL$ intersect at point $N$. Find the angle between lines $O_1A$ and $O_2N$.
Circles $\omega_1$ and $\omega_2$ with centers $O_1$ and $O_2$ respectively intersect at point $B$.The extension of the segment $O_2B$ beyond the point $B$ intersects the circle $\omega_1$ at the point $K$, and the extension of the segment $O_1B$ beyond the point $B$ intersects the circle $\omega_2$ at the point $L$. The straight line passing through $B$ parallel to $KL$ , intersects the circles $\omega_1$ and $\omega_2$ for the second time at the points $A$ and $C$, respectively. Rays $AK$ and $CL$ intersect at point $N$. Find the angle between lines $O_1N$ and $O_2B$.
Seniors Finals (grades 10-11) 3D geometry
Boy Kolya cuts off a piece of cheese in the shape of a rectangular parallelepiped with edges $2, 4, 8$, a slice for a sandwich. How many edges can a slice cut have? What is the largest cut area if it has a right angle?
original wording
Мальчик Коля отрезает от куска сыра, имеющего форму прямоугольного параллелепипеда с ребрами 2, 4, 8, ломтик на бутерброд. Сколько ребер может быть у среза ломтика? Какова наибольшая площадь среза, если он имеет прямой угол?
Amateur agronomist Petya raised three spherical tomatoes, the diameters of which are $2$ cm, $4$ cm and $6$ cm. He decided to keep the crop for history in a cylindrical vessel. Petya has $100$ cm$^2$ of preservative solution. Will Petya be able to choose a vessel so that the filled solution completely covers the tomatoes?
original wording
Агроном-любитель Петя вырастил три сферических помидора, диаметры которых равны 2 см, 4 см и 6 см. Урожай он решил сохранить для истории в сосуде цилиндрической формы. У Пети имеется 100 см2 консервирующего раствора. Сможет ли Петя подобрать сосуд так, чтобы залитый раствор полностью закрыл помидоры?
From a sheet of iron, Petya cut out a square with a side of $\sqrt{48}$ cm and four isosceles triangles with a base $\sqrt{48}$ cm and a lateral side $\sqrt{60}$ cm. These parts glued , created a regular quadrangular pyramid without gaps in the joints. It is known that with the most economical grinding, metal will go to waste. Find the thickness of the iron sheet.
original wording
Из листа железа Петя вырезал квадрат со стороной $\sqrt{48}$см и четыре равнобедренных треугольника с основанием $\sqrt{48}$ см и боковой стороной $\sqrt{60}$см. Торцы всех фигур, изначально перпендикулярные их плоскостям, Пет,я заточил на станке, после чего из полученных деталей склеил правильную четырехугольную пирамиду без зазоров в стыках. Известно, что при наиболее экономном стачивании в отходы уйдет металла. Найти толщину листа железа.
At the base of the triangular pyramid $ABCS$ of volume $\sqrt{48}$ lies an equilateral triangle $ABC$ with side $1$. The projection $K$ of the vertex $S$ onto the base of the pyramid lies at the altitude $BH$ of the triangle $ABC$, and $BK: KH = 6: 5$. Find the smallest cross-sectional area of the pyramid by the plane containing $SK$ and intersecting the segments $AB$ and $BC$.
In a spherical shell of radius $5$ are placed three metallic balls, two of which have radii $1$ and $4$. Find the maximum possible radius of the third ball.
A spherical head of Swiss cheese has holes in the form of balls of radii that do not overlap each other $1, 2.7 , ... , 2.7^n$, mm. Find the smallest possible head radius.
A cylindrical box with a flat lid is given. The lateral surface area of the box is $98\pi$ . Is it possible to place metal balls of radii $4$, $\frac{9}{4}$ and $1$?
There is a tent in the shape of a hemisphere on the plane. Three balls are placed inside the tent. The first two have a radius of $1$, touch each other, as well as the roof and the diameter of the tent base. The third ball of radius $r$ touches the other two, the roof and the base of the tent. Find $r$.
In plane stands a tent in the shape of a hemisphere. Three identical balls are placed inside the tent, which touch each other, the base of the tent and its roof. In addition, a fourth ball is placed inside the tent, which touches the roof of the tent and each of the other three balls. The tent is cut by a horizontal plane touching from above three identical balls. In what ratio will it divide the volume of the fourth ball?
Three balls of radius $r$ are placed in a cone with base radius $2$ and generatrix $4$. They touch each other (externally), the lateral surface of the cone, and the first two balls touch the base of the cone. Find the maximum value of $r$.
In a cone, whose base diameter is equal to the generatrix, are placed three identical balls, which touch each other externally. Two balls touch the side surface and the base of the cone. The third ball touches the side surface of the cone at a point lying in the same plane with the centers of the balls. Find the ratio of the radii of the base of the cone and the balls.
The cone contains four balls that touch each other (externally) and the lateral surface of the cone. Three balls have a radius of $3$ and also touch the base of the cone. Find the radius of the fourth ball if the angle between the generatrix and the base of the cone is $\frac{\pi}{3}$.
Four identical balls are placed in a cone whose base height and radius are $7$. Each of them touches the other two (externally), the base and the lateral surface of the cone. The fifth ball touches the lateral surface of the cone and all identical balls (externally). Find the radius of the fifth ball.
The area is limited by two cones with a common base, the height of which is half the generatrix. Three balls are placed in the area, contacting each other externally. Two balls are the same and touch both cones, and the third one touches the boundary of the region. What is the maximum ratio of the radius of the third ball to the radius of the first?
Three cones with vertex $A$ and generatrix $\sqrt8$ touch each other externally. For two cones, the angle between the generatrix and the axis of symmetry is $\frac{\pi}{6}$, and for the third it is $\frac{\pi}{4}$. Find the volume of the pyramid $O_1O_2O_3A$, where $O_1, O_2, O_3$ are the centers of the bases of the cones.
Three identical cones with apex $A$ touch each other externally. Each of them internally touches the fourth cone with apex at point $A$ and an apex angle $\frac{2\pi}{3}$. Find the apex angle for identical cones. (The angle at the apex of the cone is the angle between its generatrices in the axial section.)
Three cones with apex $A$ touch each other externally, and the first two of them are the same, and for the third, the angle at the vertex is equal to $\frac{\pi}{4}$. All cones also touch one plane passing through point $A$ and lie on one side of it. Find the apex angle of the first two cones. (The angle at the apex of a cone is the angle between its generatrices in the axial section.)
There are three cones on the table, touching each other. The radii of their bases are equal to $32, 48$ and $48$, and the apex angles $\frac{\pi}{3}, \frac{2\pi}{3}$ and $\frac{2\pi}{3}$ respectively (the angle at the apex of the cone is the angle between its generatrices in the axial section). A ball was suspended over the table, touching all the cones. It turned out that the center of the ball is equidistant from the centers of the bases of all the cones. Find the radius of the ball.
There are three cones on the table, touching each other. The radii of their bases are equal to $6, 24$ and $24$. A truncated cone, which has a common generatrix with each of the other cones, was placed on the table with the smaller base down. Find the radius of the smaller base of the truncated cone.
There are three cones on the table, touching each other. The heights of the cones are the same, and the radii of their bases are equal to $2r, 3r$ and $10r$. A ball of radius $2$ was placed on the table, touching all the cones. It turned out that the center of the ball is equidistant from all points of contact of the cones. Find $r$.
On the table are three balls and a cone (base to the table), touching each other externally. The radii of the balls are $20$, $40$ and $40$, and the radius of the base of the cone is $21$. Find the height of the cone.
On the table are balls of radii $4, 4, 5$, touching each other externally. The vertex of the cone $C$ is on the table, and the cone itself touches all the balls externally. Point $C$ is equidistant from the centers of two equal balls, and the cone touches the third ball perpendicular to the table. Find the angle at the top of the cone. (The angle at the apex of the cone is the angle between its generators in the axial section.
There are two balls on the table, touching each other externally. The cone touches the side of the table and both balls (externally). The top of the cone is located on the segment connecting the points of contact of the balls with the table. It is known that the rays connecting the top of the cone with the centers of the balls form equal angles with the table. Find the largest possible angle at the top of the cone. (The angle at the apex of a cone is the angle between its generatrices in the axial section.)
Three cones with a common apex, contacting each other externally, have a height of $2$ and a base radius $\sqrt3$. Two balls touch each other externally and all the cones. Find the ratio of the radii of the balls (larger to smaller).
Four cones with a common apex touch each other in pairs externally. The first two and the last two cones have the same apex angle. Find the maximum angle between the axes of symmetry of the first and third cones. (The angle at the apex of the cone is the angle between its generators in the axial section).
Four cones with a common vertex $O$ touch each other externally, and the first two and the last two of them have the same vertex angle. A fifth cone, different from the fourth, touches the first three cones externally. Find the maximum angle at the top of the fifth cone. (The angle at the apex of the cone is the angle between its generators in the axial section).
On the table are three cones with a common top, touching each other externally. The axes of symmetry of the first two cones are mutually perpendicular. Two balls are inscribed in the third cone and touch each other externally. Find the maximum ratio of the radii of the larger and smaller balls.
Two regular triangular pyramids have a common side face and have no other common points. Spheres of radius $r$ are inscribed in the pyramids. The third ball of radius $R$ externally touches both pyramids and the balls inscribed in them. Find the flat angle at the top of the pyramids if $R: r = 2: 1$.
You are given two hexagonal pyramids and one triangular one, and the side faces of all pyramids are the same. It was possible to glue the pyramids together externally "without gaps", that is, so that any two pyramids have a common edge. Find the flat angle at the top of the pyramids.
Three identical regular triangular pyramids of volume $36\sqrt2$ are cast from metal. They managed to be placed so that all pyramids have a common side edge and a common top. Find the maximum side of the base of the pyramids.
There are two regular quadrangular pyramids with base side $2$ and side edge $\sqrt{10}$. They have a common side face and have no other common points. The cone has the same vertex $S$ as the pyramids and touches them externally. Find the largest possible angle at the apex of the cone at which it is possible. (The angle at the apex of the cone is the angle between its generators in the axial section).
info of a book collecting problems 2001-05 in Russian:
А. Л. Громов, Т. О. Евдокимова, К. Ю. Лавров, Ю. В. Чурин Олимпиады
математико-механического факультета для абитуриентов. СПб.: Изд-во С.-
Петербургского университета, 2006. // Пособие содержит материалы заданий
Олимпиады 2001–2005 гг.
info of a book collecting problems 2006-12 in Russian:
А. Л. Громов, Т. О. Евдокимова, К. А. Сухов, А. И. Храбров, Ю. В. Чурин "Избранные задачи олимпиады школьников СПбГУ по математике" СПб.: Изд-во ВВМ, С.-Петерб. ун-т, 2013. // Пособие содержит материалы заданий заключительных этапов Олимпиады 2006–2012 гг.

No comments:
Post a Comment