geometry problems from Chilean Mathematical Olympiads
1989 - 2018
The lengths of the three sides of a $ \triangle ABC $ are rational. The altitude $ CD $ determines on the side $AB$ two segments $ AD $ and $ DB $. Prove that $ AD, DB $ are rational.
2006 Chile L2 P2
In a triangle $ \vartriangle ABC $ with sides integer numbers, it is known that the radius of the circumcircle circumscribed to $ \vartriangle ABC $ measures $ \dfrac {65} {8} $ centimeters and the area is $84$ cm². Determine the lengths of the sides of the triangle.
Let $ \vartriangle ABC $ be an acute triangle and scalene, with $ BC $ its smallest side. Let $ P, Q $ points on $ AB, AC $ respectively, such that $ BQ = CP = BC $. Let $ O_1, O_2 $ be the centers of the circles circumscribed to $ \vartriangle AQB, \vartriangle APC $, respectively. Sean $ H, O $ the orthocenter and circumcenter of $ \vartriangle ABC $
a) Show that $ O_1O_2 = BC $.
b) Show that $ BO_2, CO_1 $ and $ HO $ are concurrent
2007 Chile L2 P2
Given a $\triangle ABC$, determine which is the circle with the smallest area that contains it.
2007 Chile L2 P6
Given an $\triangle ABC$ isoceles with base $BC$ we note with $M$ the midpoint of said base. Let $X$ be any point on the shortest arc $AM$ of the circumcircle of $\triangle ABM$ and let $T$ be a point on the inside $\angle BMA$ such that $\angle TMX = 90^o$ and $TX = BX$. Show that $\angle MTB - \angle CTM$ does not depend on $X$.
2008 Chile L2 P2
Let $ABC$ be right isosceles triangle with right angle in $A$. Given a point $P$ inside the triangle, denote by $a, b$ and $c$ the lengths of $PA, PB$ and $PC$, respectively. Prove that there is a triangle whose sides have a length of $a\sqrt2 , b$ and $c$
2009 Chile L2 P2
Consider $P$ a regular $9$-sided convex polygon with each side of length $1$. A diagonal at $P$ is any line joining two non-adjacent vertices of $P$. Calculate the difference between the lengths of the largest and smallest diagonal of $P$.
2006 Chile Level 1 P2
The vertex $ E $ of a square $ EFGH $ of side $2006$ mm is found in the center of the square $ ABCD $ of side $10$ mm. The line $ EF $ intersects $ CD $ at point $ I $. The line$ EH $ intercepts $ AD $ in $ J $. Also $ \angle EID = 60^o$. Calculate the area of the quadrilateral $ EIDJ $.
Olimpiada de Matemática de Chile
original wordings: 1989 - 2011
collected in aops here
Olimpiada de Matemática de Chile
[missing are 2017 L1+ L2]
olympiad started in 1989
level 1 started in 1999
In a right triangle with legs $a$, $b$ and hypotenuse $c$, draw semicircles with diameters on the sides of the triangle as indicated in the figure. The purple areas have values $X,Y$ . Calculate $X + Y$.
The lengths of the three sides of a $ \triangle ABC $ are rational. The altitude $ CD $ determines on the side $AB$ two segments $ AD $ and $ DB $. Prove that $ AD, DB $ are rational.
1990 Chile P6
Given a regular polygon with apothem $ A $ and circumradius $ R $. Find a regular polygon of equal perimeter and with double sides, the apothem $ a $ and the circumcircle $ r $.
Given a regular polygon with apothem $ A $ and circumradius $ R $. Find a regular polygon of equal perimeter and with double sides, the apothem $ a $ and the circumcircle $ r $.
1991 Chile P2
If a polygon inscribed in a circle is equiangular and has an odd number of sides, prove that it is regular.
If a polygon inscribed in a circle is equiangular and has an odd number of sides, prove that it is regular.
1991 Chile P6
Given a triangle with $ \triangle ABC $, with: $ \angle C = 36^o$ and $ \angle A = \angle B $. Consider the points $ D $ on $ BC $, $ E $ on $ AD $, $ F $ on $ BE $, $ G $ on $ DF $ and $ H $ on $ EG $, so that the rays $ AD, BE, DF, EG, FH $ bisect the angles $ A, B, D, E, F $ respectively. It is known that $ FH = 1 $. Calculate $ AC$.
Given a triangle with $ \triangle ABC $, with: $ \angle C = 36^o$ and $ \angle A = \angle B $. Consider the points $ D $ on $ BC $, $ E $ on $ AD $, $ F $ on $ BE $, $ G $ on $ DF $ and $ H $ on $ EG $, so that the rays $ AD, BE, DF, EG, FH $ bisect the angles $ A, B, D, E, F $ respectively. It is known that $ FH = 1 $. Calculate $ AC$.
1992 Chile P4
Given three parallel lines, prove that there are three points, one on each line, which are the vertices of an equilateral triangle.
Given three parallel lines, prove that there are three points, one on each line, which are the vertices of an equilateral triangle.
1992 Chile P5
In the $\triangle ABC $, points $ M, I, H $ are feet, respectively, of the median, bisector and height, drawn from $ A $. It is known that $ BC = 2 $, $ MI = 2-\sqrt {3} $ and $ AB > AC $.
a) Prove that $ I$ lies between $ M $ and $ H $.
b) Calculate $ AB ^ 2-AC ^ 2 $.
c) Determine $ \dfrac {AB} {AC} $.
d) Find the measure of all the sides and angles of the triangle.
In the $\triangle ABC $, points $ M, I, H $ are feet, respectively, of the median, bisector and height, drawn from $ A $. It is known that $ BC = 2 $, $ MI = 2-\sqrt {3} $ and $ AB > AC $.
a) Prove that $ I$ lies between $ M $ and $ H $.
b) Calculate $ AB ^ 2-AC ^ 2 $.
c) Determine $ \dfrac {AB} {AC} $.
d) Find the measure of all the sides and angles of the triangle.
1993 Chile P1
There are four houses, located on the vertices of a square. You want to draw a road network, so that you can go from any house to any other. Prove that the network formed by the diagonals is not the shortest. Find a shorter network.
1993 Chile P2
Given a rectangle, circumscribe a rectangle of maximum area.
1993 Chile P6
There are four houses, located on the vertices of a square. You want to draw a road network, so that you can go from any house to any other. Prove that the network formed by the diagonals is not the shortest. Find a shorter network.
Given a rectangle, circumscribe a rectangle of maximum area.
1993 Chile P6
Let $ ABCD $ be a rectangle of area $ S $, and $ P $ be a point inside it. We denote by $ a, b, c, d $ the distances from $ P $ to the vertices $ A, B, C, D $ respectively. Prove that $ a ^ 2 + b ^ 2 + c ^ 2 + d ^ 2\ge 2S $. When there is equality?
1994 Chile P2
Show that it is possible to cut any triangle into several pieces, so that a rectangle is formed when they are joined together.
Show that it is possible to cut any triangle into several pieces, so that a rectangle is formed when they are joined together.
1994 Chile P6
On a sheet of transparent paper, draw a quadrilateral with Chinese ink, which is illuminated with a lamp. Show that it is always possible to locate the sheet in such a way that the shadow projected on the desk is a parallelogram.
1995 Chile P2
In a circle of radius $1$, six arcs of radius $1$ are drawn, which cut the circle as in the figure. Determine the black area.
On a sheet of transparent paper, draw a quadrilateral with Chinese ink, which is illuminated with a lamp. Show that it is always possible to locate the sheet in such a way that the shadow projected on the desk is a parallelogram.
1995 Chile P2
In a circle of radius $1$, six arcs of radius $1$ are drawn, which cut the circle as in the figure. Determine the black area.
1995 Chile P7
In a semicircle of radius 4 three circles are inscribed, as indicated in the figure. Larger circles have radii $ R_1 $ and $ R_2 $, and the larger circle has radius $ r $.
a) Prove that $ \dfrac {1} {\sqrt{r}} = \dfrac {1} {\sqrt{R_1}} + \dfrac {1} {\sqrt{R_2}} $
b) Prove that $ R_1 + R_2 \le 8 (\sqrt{2} -1) $
c) Prove that $ r \le \sqrt{2} -1 $
In a semicircle of radius 4 three circles are inscribed, as indicated in the figure. Larger circles have radii $ R_1 $ and $ R_2 $, and the larger circle has radius $ r $.
a) Prove that $ \dfrac {1} {\sqrt{r}} = \dfrac {1} {\sqrt{R_1}} + \dfrac {1} {\sqrt{R_2}} $
b) Prove that $ R_1 + R_2 \le 8 (\sqrt{2} -1) $
c) Prove that $ r \le \sqrt{2} -1 $
1996 Chile P2
Construct the $ \triangle ABC $, with $ AC <BC $, if the circumcircle is known, and the points $ D, E, F $ in it, where they intersect, respectively, the height, the median and the bisector that they start from the vertex $ C $.
1996 Chile P6
Two circles, $ C $ and $ K $, intersect at $ A $ and $ B $. Let $ P $ a point in the arc $ AB $ in $ C $. Lines $ PA $ and $ PB $ cut back to $ K $ in $ R $ and $ S $, respectively. Let $ P_1 $ be another point in the same arc as $ P $, so that lines $ P_1A $ and $ P_1B $ re-intersect $ K $ in $ R_1 $ and $ S_1 $, respectively. Prove that the arcs $ RS $ and $ R_1S_1 $ have equal measure.
Construct the $ \triangle ABC $, with $ AC <BC $, if the circumcircle is known, and the points $ D, E, F $ in it, where they intersect, respectively, the height, the median and the bisector that they start from the vertex $ C $.
1996 Chile P6
Two circles, $ C $ and $ K $, intersect at $ A $ and $ B $. Let $ P $ a point in the arc $ AB $ in $ C $. Lines $ PA $ and $ PB $ cut back to $ K $ in $ R $ and $ S $, respectively. Let $ P_1 $ be another point in the same arc as $ P $, so that lines $ P_1A $ and $ P_1B $ re-intersect $ K $ in $ R_1 $ and $ S_1 $, respectively. Prove that the arcs $ RS $ and $ R_1S_1 $ have equal measure.
1997 Chile P3
Let $ ABCD $ be a quadrilateral, whose diagonals intersect at $ O $. The triangles $ \triangle AOB $, $ \triangle BOC $, $ \triangle COD $ have areas $1, 2, 4$, respectively. Find the area of $ \triangle AOD $ and prove that $ ABCD $ is a trapezoid.
Let $ ABCD $ be a quadrilateral, whose diagonals intersect at $ O $. The triangles $ \triangle AOB $, $ \triangle BOC $, $ \triangle COD $ have areas $1, 2, 4$, respectively. Find the area of $ \triangle AOD $ and prove that $ ABCD $ is a trapezoid.
1997 Chile P5
Let: $ C_1, C_2, C_3 $ three circles , intersecting in pairs, such that the secant line common to two of them (any) passes through the center of the third. Prove that the three lines thus defined are concurrent.
Let: $ C_1, C_2, C_3 $ three circles , intersecting in pairs, such that the secant line common to two of them (any) passes through the center of the third. Prove that the three lines thus defined are concurrent.
1998 Chile P2
Given a semicircle of diameter $ AB $, with $ AB = 2r $, be $ CD $ a variable string, but of fixed length $ c $. Let $ E $ be the intersection point of lines $ AC $ and $ BD $, and let $ F $ be the intersection point of lines $ AD $ and $ BC $.
a) Prove that the lines $ EF $ and $ AB $ are perpendicular.
b) Determine the locus of the point $ E $.
c) Prove that $ EF $ has a constant measure, and determine it based on $ c $ and $ r $.
Given a semicircle of diameter $ AB $, with $ AB = 2r $, be $ CD $ a variable string, but of fixed length $ c $. Let $ E $ be the intersection point of lines $ AC $ and $ BD $, and let $ F $ be the intersection point of lines $ AD $ and $ BC $.
a) Prove that the lines $ EF $ and $ AB $ are perpendicular.
b) Determine the locus of the point $ E $.
c) Prove that $ EF $ has a constant measure, and determine it based on $ c $ and $ r $.
1998 Chile P6
To create an equilateral triangle, cut it into four polygonal figures so that, reassembled properly, these figures form a square.
To create an equilateral triangle, cut it into four polygonal figures so that, reassembled properly, these figures form a square.
In an acute triangle $ABC$, let $ \overline {AK}, \overline {BL}, \overline {CM} $ be the altitudes of the triangle concurrent at the point $ H $ and let $ P $ the midpoint of $ \overline {AH} $. Let's define $ S = \overline {BH} \cap \overline {MK} $ and $ T = \overline {LP} \cap \overline {AB} $. Show that $ \overline {TS} \perp \overline {BC} $
1999 Chile L2 P6
Prove that there are infinite pairs of non-congruent triangles that have the same angles and two of their equal sides. Develop an algorithm or rule to obtain these pairs of triangles and indicate at least one pair that satisfies the asserted.
Prove that there are infinite pairs of non-congruent triangles that have the same angles and two of their equal sides. Develop an algorithm or rule to obtain these pairs of triangles and indicate at least one pair that satisfies the asserted.
In the plane, we have any polygon that does not intersect itself and is closed. Given a point that is not on the edge of the polygon. How can we determine whether it is inside or outside the polygon? (the polygon has a finite number of sides)
2000 Chile L2 P4
Let $ AD $ be the bisector of a triangle $ ABC $ $ (D \in BC) $ such that $ AB + AD = CD $ and $ AC + AD = BC $. Determine the measure of the angles of $ \vartriangle ABC $
Let $ AD $ be the bisector of a triangle $ ABC $ $ (D \in BC) $ such that $ AB + AD = CD $ and $ AC + AD = BC $. Determine the measure of the angles of $ \vartriangle ABC $
In a triangle $ \vartriangle ABC $, let $ h_a, h_b $ and $ h_c $ the atlitudes. Let $ D $ be the point where the inner bisector of $ \angle BAC $ cuts to the side $ BC $ and $ d_a $ is the distance from the $ D $ point next to $ AB $. The distances $ d_b $ and $ d_c $ are similarly defined. Show that:
$$ \dfrac {3} {2} \le \dfrac {d_a} {h_a} + \dfrac {d_b} {h_b} + \dfrac {d_c} {h_c} $$
For what kind of triangles does the equality hold?
$$ \dfrac {3} {2} \le \dfrac {d_a} {h_a} + \dfrac {d_b} {h_b} + \dfrac {d_c} {h_c} $$
For what kind of triangles does the equality hold?
On a right triangle of paper, two points $A$ and $B$ have been painted. You have scissors and you have the right to make cuts (on paper) as follows: cut through a height of the given triangle. In doing so, remove, without the respective altitude, one of the two triangles and continue the process. Prove that after a finite number of cuts you can separate points $A$ and $B$ leaving one of them outside the remaining triangles.
2001 Chile L2 P6
Let $ C_1, C_2 $ be two circles of equal radius, disjoint, of centers $ O_1, O_2 $, such that $ C_1 $ is to the left of $ C_2 $. Let $ l $ be a line parallel to the line $ O_1O_2 $, secant to both circles. Let $ P_1 $ be a point of $ l $, to the left of $ C_1 $ and $ P_2 $ a point of $ l $, to the right of $ C_2 $ such that the tangents of $ P_1 $ to $ C_1 $ and of $ P_2 $ a $ C_2 $ form a quadrilateral. Show that there is a circle tangent to the four sides of said quadrilateral.
Let $ C_1, C_2 $ be two circles of equal radius, disjoint, of centers $ O_1, O_2 $, such that $ C_1 $ is to the left of $ C_2 $. Let $ l $ be a line parallel to the line $ O_1O_2 $, secant to both circles. Let $ P_1 $ be a point of $ l $, to the left of $ C_1 $ and $ P_2 $ a point of $ l $, to the right of $ C_2 $ such that the tangents of $ P_1 $ to $ C_1 $ and of $ P_2 $ a $ C_2 $ form a quadrilateral. Show that there is a circle tangent to the four sides of said quadrilateral.
2002 Chile L2 P3
Given the segment $ AB $, let $ M $ be one point lying on it. Towards the same side of the plane and with base $ AM $ and $ MB $, the squares $ AMCD $ and $ MBEF $ are constructed. Let $ P $ and $ Q $ be the respective centers of these squares. Determine how the midpoint of the segment $ PQ $ moves as the point $ M $ moves aling the segment.
Given the segment $ AB $, let $ M $ be one point lying on it. Towards the same side of the plane and with base $ AM $ and $ MB $, the squares $ AMCD $ and $ MBEF $ are constructed. Let $ P $ and $ Q $ be the respective centers of these squares. Determine how the midpoint of the segment $ PQ $ moves as the point $ M $ moves aling the segment.
Given a right triangle $T$, where the coordinates of its vertices are integers, let $E$ be the number of points of integer coordinates that belong to the edge of the triangle $T$, $I$ the number of points of integer coordinates that belong to the interior of the triangle $T$. Show that the area $A(T)$ of triangle $T$ is given by: $A(T) = \frac{E}{2}+I -1$.
Consider a triangle $ ABC $. On the line $ AC $ take a point $ B_1 $ such that $ AB = AB_1 $ and in addition, $ B_1 $ and $ C $ are located on the same side of the line with respect to the point $ A $. The bisector of the angle $ A $ intersects the side $ BC $ at a point that we will denote as $ A_1 $. Let $ P $ and $ R $ be the circumscribed circles of the triangles $ ABC $ and $ A_1B_1C $ respectively. They intersect at points $ C $ and $ Q $. Prove that the tangent to the circle $ R $ at the point $ Q $ is parallel to the line $ AC $.
2004 Chile L2 P3
The perimeter, that is, the sum of the lengths of all sides of a convex quadrilateral $ ABCD $, is equal to $2004$ meters; while the length of its diagonal $ AC $ is equal to $1001$ meters. Find out if the length of the other diagonal $ BD $ can:
a) To be equal to only one meter.
b) Be equal to the length of the diagonal $ AC $.
The perimeter, that is, the sum of the lengths of all sides of a convex quadrilateral $ ABCD $, is equal to $2004$ meters; while the length of its diagonal $ AC $ is equal to $1001$ meters. Find out if the length of the other diagonal $ BD $ can:
a) To be equal to only one meter.
b) Be equal to the length of the diagonal $ AC $.
2004 Chile L2 P6
The $ AB, BC $ and $ CD $ segments of the polygon $ ABCD $ have the same length and are tangent to a circle $ S $, centered on the point $ O $. Let $ P $ be the point of tangency of $ BC $ with $ S $, and let $ Q $ be the intersection point of lines $ AC $ and $ BD $. Show that the point $ Q $ is collinear with the points $ P $ and $ O $.
The $ AB, BC $ and $ CD $ segments of the polygon $ ABCD $ have the same length and are tangent to a circle $ S $, centered on the point $ O $. Let $ P $ be the point of tangency of $ BC $ with $ S $, and let $ Q $ be the intersection point of lines $ AC $ and $ BD $. Show that the point $ Q $ is collinear with the points $ P $ and $ O $.
In the center of the square of side 1 that shows the figure is an ant. At one point the ant begins to walk until it touches the left side (a), then continues walking until it reaches the bottom side (b) and finally returns to the starting point. Show that, regardless of the path followed by the ant, the distance it travels is greater than the square root of 2.
In a triangle $ \vartriangle ABC $ with sides integer numbers, it is known that the radius of the circumcircle circumscribed to $ \vartriangle ABC $ measures $ \dfrac {65} {8} $ centimeters and the area is $84$ cm². Determine the lengths of the sides of the triangle.
Let $ \vartriangle ABC $ be an acute triangle and scalene, with $ BC $ its smallest side. Let $ P, Q $ points on $ AB, AC $ respectively, such that $ BQ = CP = BC $. Let $ O_1, O_2 $ be the centers of the circles circumscribed to $ \vartriangle AQB, \vartriangle APC $, respectively. Sean $ H, O $ the orthocenter and circumcenter of $ \vartriangle ABC $
a) Show that $ O_1O_2 = BC $.
b) Show that $ BO_2, CO_1 $ and $ HO $ are concurrent
2007 Chile L2 P2
Given a $\triangle ABC$, determine which is the circle with the smallest area that contains it.
Given an $\triangle ABC$ isoceles with base $BC$ we note with $M$ the midpoint of said base. Let $X$ be any point on the shortest arc $AM$ of the circumcircle of $\triangle ABM$ and let $T$ be a point on the inside $\angle BMA$ such that $\angle TMX = 90^o$ and $TX = BX$. Show that $\angle MTB - \angle CTM$ does not depend on $X$.
2008 Chile L2 P2
Let $ABC$ be right isosceles triangle with right angle in $A$. Given a point $P$ inside the triangle, denote by $a, b$ and $c$ the lengths of $PA, PB$ and $PC$, respectively. Prove that there is a triangle whose sides have a length of $a\sqrt2 , b$ and $c$
2009 Chile L2 P2
Consider $P$ a regular $9$-sided convex polygon with each side of length $1$. A diagonal at $P$ is any line joining two non-adjacent vertices of $P$. Calculate the difference between the lengths of the largest and smallest diagonal of $P$.
2010 Chile L2 P3
The sides $BC, CA$, and $AB$ of a triangle $ABC$ are tangent to a circle at points $X, Y, Z$ respectively. Show that the center of such a circle is on the line that passes through the midpoints of $BC$ and $AX$.
The sides $BC, CA$, and $AB$ of a triangle $ABC$ are tangent to a circle at points $X, Y, Z$ respectively. Show that the center of such a circle is on the line that passes through the midpoints of $BC$ and $AX$.
2010 Chile L2 P5
Consider a line $ \ell $ in the plane and let $ B_1, B_2, B_3 $ be different points in $ \ell$. Let $ A $ be a point that is not in $ \ell$. Show that there is $ P, Q $ in $ {B_1, B_2, B_3} $ with $ P \ne Q $ so that the distance from $ A $ to $ \ell$ is greater than the distance from $ P $ to the line that passes through $ A $ and $ Q $.
Consider a line $ \ell $ in the plane and let $ B_1, B_2, B_3 $ be different points in $ \ell$. Let $ A $ be a point that is not in $ \ell$. Show that there is $ P, Q $ in $ {B_1, B_2, B_3} $ with $ P \ne Q $ so that the distance from $ A $ to $ \ell$ is greater than the distance from $ P $ to the line that passes through $ A $ and $ Q $.
2011 Chile L2 P2
Let $O$ be the center of the circle circumscribed to triangle $ABC$ and let $ S_ {A} $, $ S_ {B} $, $ S_ {C} $ be the circles centered on $O$ that are tangent to the sides $BC, CA, AB$ respectively. Show that the sum of the angle between the two tangents $ S_ {A} $ from $A$ plus the angle between the two tangents $ S_ {B} $ from $B$ plus the angle between the two tangents $ S_ {C} $ from $C$ is $180$ degrees.
Let $O$ be the center of the circle circumscribed to triangle $ABC$ and let $ S_ {A} $, $ S_ {B} $, $ S_ {C} $ be the circles centered on $O$ that are tangent to the sides $BC, CA, AB$ respectively. Show that the sum of the angle between the two tangents $ S_ {A} $ from $A$ plus the angle between the two tangents $ S_ {B} $ from $B$ plus the angle between the two tangents $ S_ {C} $ from $C$ is $180$ degrees.
2012 Chile L2 P4
Consider an isosceles triangle $ABC$, where $AB = AC$. $D$ is a point on the $AC$ side and $P$ a point on the segment $BD$ so that the angle $\angle APC = 90^o$ and $ \angle ABP = \angle BCP $. Determine the ratio $AD: DC$.
Consider an isosceles triangle $ABC$, where $AB = AC$. $D$ is a point on the $AC$ side and $P$ a point on the segment $BD$ so that the angle $\angle APC = 90^o$ and $ \angle ABP = \angle BCP $. Determine the ratio $AD: DC$.
A conical surface $ C $ is cut by a plane $ T $ as shown in the figure on the back of this sheet. Show that $ C \cap T $ is an ellipse. You can use as an aid the fact that if you consider the two spheres tangent to $ C $ and $ T $ as shown in the figure, they intersect $ T $ in the bulbs.
2014 Chile L2 P2
Consider an $ABCD$ parallelogram of area $1$. Let $E$ be the center of gravity of the triangle $ABC, F$ the center of gravity of the triangle $BCD, G$ the center of gravity of the triangle $CDA$ and $H$ the center of gravity of the triangle $DAB$. Calculate the area of quadrilateral $EFGH$.
2014 Chile L2 P2
Consider an $ABCD$ parallelogram of area $1$. Let $E$ be the center of gravity of the triangle $ABC, F$ the center of gravity of the triangle $BCD, G$ the center of gravity of the triangle $CDA$ and $H$ the center of gravity of the triangle $DAB$. Calculate the area of quadrilateral $EFGH$.
2015 Chile L1 P1, L2 P1
On the plane, there is drawn a parallelogram $P$ and a point $X$ outside of $P$. Using only an ungraded rule, determine the point $W$ that is symmetric to $X$ with respect to the center $O$ of $P$.
On the plane, there is drawn a parallelogram $P$ and a point $X$ outside of $P$. Using only an ungraded rule, determine the point $W$ that is symmetric to $X$ with respect to the center $O$ of $P$.
2015 Chile L1 P5, L2 P5
A quadrilateral $ABCD$ is inscribed in a circle. Suppose that $|DA| =|BC|= 2$ and$ |AB| = 4$. Let $E $be the point of intersection of lines$ BC$ and $DA$. Suppose that $\angle AEB = 60^o$ and that $|CD| <|AB|$. Calculate the radius of the circle.
A quadrilateral $ABCD$ is inscribed in a circle. Suppose that $|DA| =|BC|= 2$ and$ |AB| = 4$. Let $E $be the point of intersection of lines$ BC$ and $DA$. Suppose that $\angle AEB = 60^o$ and that $|CD| <|AB|$. Calculate the radius of the circle.
2016 Chile L1 P2, L2 P2
For an equilateral triangle $\triangle ABC$, determine whether or not there is a point $P$ inside $\triangle ABC$ so that any straight line that passes through $P$ divides the triangle $\triangle ABC$ in two polygonal lines of equal length.
2016 Chile L2 P6
Let $P_1$ and $P_2$ be two non-parallel planes in space, and $A$ a point that does not It is in none of them. For each point $X$, let $X_1$ denote its reflection with respect to $P_1$, and $X_2$ its reflection with respect to $P_2$. Determine the locus of points $X$ for the which $X_1, X_2$ and $A$ are collinear.
For an equilateral triangle $\triangle ABC$, determine whether or not there is a point $P$ inside $\triangle ABC$ so that any straight line that passes through $P$ divides the triangle $\triangle ABC$ in two polygonal lines of equal length.
2016 Chile L2 P6
Let $P_1$ and $P_2$ be two non-parallel planes in space, and $A$ a point that does not It is in none of them. For each point $X$, let $X_1$ denote its reflection with respect to $P_1$, and $X_2$ its reflection with respect to $P_2$. Determine the locus of points $X$ for the which $X_1, X_2$ and $A$ are collinear.
2017 missing
Consider $ABCD$ a square of side $1$. Points $P, Q, R,S$ are chosen in the sides $AB, BC, CD. DA$ respectively in such a way that $ |AP| = |BQ| = |CR| =|DS| = a$, with $a <1$. Segments $AQ, BR, CS$ and $DP$ are plotted. Calculate the area of the other quadrilateral , that is formed in the center of the figure.
2018 Chile L2 P6
Consider an acute triangle $ABC$ and its altitudes from $A$ and $B$ that intersect the respective sides in $D$ and $E$. Call $H$ the point of intersection of the altitudes . A circle is constructed with center in $H$ and radius $HE$. Let $C$ be a line tangent to the circle at point $P$. With center at $B$ and radio $BE$ another circle is plotted, and from $C$ another line is drawn tangent to the this circle at point $Q$. Show that points $D, P$, and $Q$ are collinear.
Consider an acute triangle $ABC$ and its altitudes from $A$ and $B$ that intersect the respective sides in $D$ and $E$. Call $H$ the point of intersection of the altitudes . A circle is constructed with center in $H$ and radius $HE$. Let $C$ be a line tangent to the circle at point $P$. With center at $B$ and radio $BE$ another circle is plotted, and from $C$ another line is drawn tangent to the this circle at point $Q$. Show that points $D, P$, and $Q$ are collinear.
In the convex quadrilateral $ABCD$ , $\angle ADC = \angle BCD > 90^o$ . Let $E$ be the intersection of the line $AC$ with the line parallel to $AD$ that passes through $B$. Let $F$ be the intersection of line $BD$ with the line parallel to $BC$ passing through $A$. Prove that $EF$ is parallel to $CD$.
Given the isosceles triangle ABC with $| AB | = | AC | = 10$ and $| BC | = 15$. Let points $P$ in $BC$ and $Q$ in $AC$ chosen such that $| AQ | = | QP | = | P C |$. Calculate the ratio of areas of the triangles $(PQA): (ABC)$.
Level 1 (nivel menor)
1999 Chile Level 1 P2
Given a pararellelogram $ ABCD $, let $ E, F $ be the midpoints of the sides $BC$ and $CD$, respectively. Prove that $ AE $ and $AF$ trisect to $BD$.
Given a pararellelogram $ ABCD $, let $ E, F $ be the midpoints of the sides $BC$ and $CD$, respectively. Prove that $ AE $ and $AF$ trisect to $BD$.
1999 Chile Level 1 P5
For the rectangles in the figure we know that $a:b=1:3$ . Find the value of the ratio of the areas of the triangles $\triangle BEC , \triangle DCF$
For the rectangles in the figure we know that $a:b=1:3$ . Find the value of the ratio of the areas of the triangles $\triangle BEC , \triangle DCF$
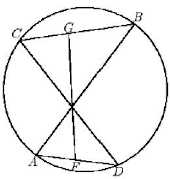
In the figure, $AD$ and $CB$ are two chords of a circle, which intersect at $E$, and $FG$ is the bisector of $\angle AED$. Show that $AF \cdot BG = CG \cdot FD$.
2000 Chile Level 1 P5
A point $ P $ interior to a $ \vartriangle ABC $ satisfies: $ \angle PBA = \angle PCA = \dfrac {1} {3} (\angle ABC + \angle ACB) $. Prove that $ \dfrac {AC + PB} {AB} = \dfrac {AB + PC} {AC} $
A point $ P $ interior to a $ \vartriangle ABC $ satisfies: $ \angle PBA = \angle PCA = \dfrac {1} {3} (\angle ABC + \angle ACB) $. Prove that $ \dfrac {AC + PB} {AB} = \dfrac {AB + PC} {AC} $
2001 Chile Level 1 P5
The segment $ AB $ measures $9$ cm. and the point $ C $ lies on it, such that $ \dfrac {AC} {CB} = 2 $. The point $ D $ is such that $ \angle ACD = 60^o$ and $ \angle ABD = 45^o$. Determine the measures of the angles of the triangles $ \vartriangle ACD, \vartriangle CBD $ and $ \vartriangle ABD $.
The segment $ AB $ measures $9$ cm. and the point $ C $ lies on it, such that $ \dfrac {AC} {CB} = 2 $. The point $ D $ is such that $ \angle ACD = 60^o$ and $ \angle ABD = 45^o$. Determine the measures of the angles of the triangles $ \vartriangle ACD, \vartriangle CBD $ and $ \vartriangle ABD $.
If in the $ \vartriangle ABC $, two sides are not greater than their corresponding altitudes, how much do the angles of the triangle measure?
Given a right triangle $T$, where the coordinates of its vertices are integers, let $E$ be the number of points of integer coordinates that belong to the edge of the triangle $T$, $I$ the number of points of integer coordinates that belong to the interior of the triangle $T$. Show that the area $A(T)$ of triangle $T$ is given by: $A(T) = \frac{E}{2}+I -1$.
Given the segment $ AB $, let $ M $ be one point lying on it. Towards the same side of the plane and with base $ AM $ and $ MB $, the squares $ AMCD $ and $ MBEF $ are constructed. Let $ P $ and $ Q $ be the respective centers of these squares. Determine how the midpoint of the segment $ PQ $ moves as the point $ M $ moves along the segment.
2003 Chile Level 1 P4
Investigate if there exists a tetrahedron $ ABCD $ such that all its faces are different isosceles triangles.
Investigate if there exists a tetrahedron $ ABCD $ such that all its faces are different isosceles triangles.
2004 missing
2005 Chile Level 1 P3
Within a square, $2$ different points are chosen. Then, $8$ line segments are drawn connecting each of these points with the vertices of the square. Is it possible to divide this square into $9$ parts with equal area?
Within a square, $2$ different points are chosen. Then, $8$ line segments are drawn connecting each of these points with the vertices of the square. Is it possible to divide this square into $9$ parts with equal area?
The vertex $ E $ of a square $ EFGH $ of side $2006$ mm is found in the center of the square $ ABCD $ of side $10$ mm. The line $ EF $ intersects $ CD $ at point $ I $. The line$ EH $ intercepts $ AD $ in $ J $. Also $ \angle EID = 60^o$. Calculate the area of the quadrilateral $ EIDJ $.
$AB = 3$, $AC = 8$, $A_1$ midpoint of $AC$, $BA_1 \parallel B_1A_2 \parallel B_2A_3$, ... $AB\perp AC$, $A_1B_1\perp AC$, $A_2B_2\perp AC$, $A_3B_3\perp AC$ ...
Find $2^9 (BA_1 + B_1A_2 + B_2A_3 + ... + B_8A_9)$
2006 Chile Level 1 P5
Let $\vartriangle ABC $ be any triangle and $ \vartriangle MNP $ the triangle formed by the tangent points of the inscribed circle with the sides of the triangle $ \vartriangle ABC $, show that if $ \vartriangle MNP $ is equilateral, then the $\vartriangle ABC $ is equilateral.
Let $\vartriangle ABC $ be any triangle and $ \vartriangle MNP $ the triangle formed by the tangent points of the inscribed circle with the sides of the triangle $ \vartriangle ABC $, show that if $ \vartriangle MNP $ is equilateral, then the $\vartriangle ABC $ is equilateral.
From a triangle $T = \triangle ABC$, we build the triangle $T_1 = \triangle A_1B_1C_1$ whose vertices they are the midpoints of the sides of $T$. The triangle $T_2 = \triangle A_2B_2C_2$ is constructed from $T_1$ in a way analogue. We build the triangles $T_3, T_4,..., T_{2007}$. Prove that the center of gravity $G$ of the triangle $T$ is inside the triangle $T_{2007}$.
2008 Chile Level 1 P2
In a circle of radius $1$ a diameter $PQ$ is drawn and an equilateral triangle with base $AB$ parallel to $PQ$ is inscribed. The segment $PQ$ cuts to the side $BC$ at the point $R$. Is the length $PR$ smaller, equal, or greater than the length of a quarter of the circumference?
2009 Chile Level 1 P1
Consider a triangle whose sides measure $1, r$, and $r^2$.
Determine all the values of $r$ in such a way that the triangle is right.
Consider a triangle whose sides measure $1, r$, and $r^2$.
Determine all the values of $r$ in such a way that the triangle is right.
2009 Chile Level 1 P2
Consider three points inside a square on side $1$.
Show that the area of the triangle they form is less than or equal to $\frac{1}{2}$.
Consider three points inside a square on side $1$.
Show that the area of the triangle they form is less than or equal to $\frac{1}{2}$.
On the base $AC$ of a triangle angle isosceles $ABC$, a point is taken $M$, so that $| AM | = p$ and $| MC | = q$. The inscribed circles are drawn to the $AMB$ and $CMB$ triangles, which are tangent to the $BM$ side at points $R$ and $S$ respectively. Find the distance between $R$ and $S$.
2010 Chile Level 1 P3
Let $ABCD$ be a square and $M$ be its center. Consider the point $E$ on line $AC$ such that $| MC | = | CE |$. Let $S$ be the circle circumscribed to triangle $\triangle EDB$. Show that $S$ passes through the midpoint of $AM$.
2010 Chile Level 1 P6
Consider a line $L$ in the plane and let $B_1, B_2, B_3$ be points different in $L$. Let $A$ be a point that does not lie in $L$. Show that there are $P, Q$ in $\{B_1, B_2, B_3\}$ with $P \ne Q$ such that the distance from $A$ to $L$ to be greater than the distance from $P$ to the line that passes through $A$ and $Q$.
Consider a line $L$ in the plane and let $B_1, B_2, B_3$ be points different in $L$. Let $A$ be a point that does not lie in $L$. Show that there are $P, Q$ in $\{B_1, B_2, B_3\}$ with $P \ne Q$ such that the distance from $A$ to $L$ to be greater than the distance from $P$ to the line that passes through $A$ and $Q$.
2011 Chile Level 1 P2
Inside a cube of side $1$, two spheres are introduced that are tangent externally to each other and such that each is tangent to three faces of the cube. Determine the greater distance to which the centers of the spheres can be found.
Inside a cube of side $1$, two spheres are introduced that are tangent externally to each other and such that each is tangent to three faces of the cube. Determine the greater distance to which the centers of the spheres can be found.
2013 Chile Level 1 P5
Four points $A, B, C, D$ move in space so that always is satisfied $(AB) = (AC) =(DB) =(DC) = 1$,
- What is the greatest value that the sum $(AD)+(BC)$ can become?
- Under what conditions is this sum maximized?
Four points $A, B, C, D$ move in space so that always is satisfied $(AB) = (AC) =(DB) =(DC) = 1$,
- What is the greatest value that the sum $(AD)+(BC)$ can become?
- Under what conditions is this sum maximized?
2014 Chile Level 1 P2
The points $P,Q,R$ are the midpoints of the sides $BC,CD$ and $DA$ of a rectangle $ABCD$ respectively and $M$ is the midpoint of the segment $QR$. The area of the rectangle is $320$. Calculate the area of the triangle $APM$ .
2015 Chile Level 1 P1
On the plane, there is drawn a parallelogram $P$ and a point $X$ outside of $P$. Using only an ungraded rule, determine the point $W$ that is symmetric to $X$ with respect to the center $O$ of $P$.
The points $P,Q,R$ are the midpoints of the sides $BC,CD$ and $DA$ of a rectangle $ABCD$ respectively and $M$ is the midpoint of the segment $QR$. The area of the rectangle is $320$. Calculate the area of the triangle $APM$ .
2015 Chile Level 1 P1
On the plane, there is drawn a parallelogram $P$ and a point $X$ outside of $P$. Using only an ungraded rule, determine the point $W$ that is symmetric to $X$ with respect to the center $O$ of $P$.
Consider a triangle $\triangle ABC$ and a point $D$ in segment $BC$. The triangles $\triangle ABD$ and $\triangle ADC$ are similar in ratio $\frac{1}{\sqrt3}$. Determine the angles of the triangle $\triangle ABC$.
2015 Chile Level 1 P5, Level 2 P5
A quadrilateral $ABCD$ is inscribed in a circle. Suppose that $|DA| =|BC|= 2$ and$ |AB| = 4$. Let $E $be the point of intersection of lines$ BC$ and $DA$. Suppose that $\angle AEB = 60^o$ and that $|CD| <|AB|$. Calculate the radius of the circle.
A quadrilateral $ABCD$ is inscribed in a circle. Suppose that $|DA| =|BC|= 2$ and$ |AB| = 4$. Let $E $be the point of intersection of lines$ BC$ and $DA$. Suppose that $\angle AEB = 60^o$ and that $|CD| <|AB|$. Calculate the radius of the circle.
2016 Chile Level 1 P2, Level 2 P2
For an equilateral triangle $\triangle ABC$, determine whether or not there is a point $P$ inside $\triangle ABC$ so that any straight line that passes through $P$ divides the triangle $\triangle ABC$ in two polygonal lines of equal length.
For an equilateral triangle $\triangle ABC$, determine whether or not there is a point $P$ inside $\triangle ABC$ so that any straight line that passes through $P$ divides the triangle $\triangle ABC$ in two polygonal lines of equal length.
2016 Chile Level 1 P5
Let $\vartriangle ABC$ be an isosceles triangle with $AC = BC$. Let $O$ be the center of the circle circumscribed to the triangle and $I$ the center of the inscribed circle. If $D$ is the point on side $BC$ such that $OD$ is perpendicular to $BI$. Show that $ID$ is parallel to $AC$.
2016 Chile Level 1 P5
Let $\triangle ABC$ be a triangle isosceles with $AC = BC$. Let $O$ be the center of circumcircle circumscribed to the triangle and $I$ the center of the inscribed circle. If $D$ is the point on the side $BC$ such that $OD$ is perpendicular to $BI$. Show that $ID$ is parallel to $AC$.
Let $\triangle ABC$ be a triangle isosceles with $AC = BC$. Let $O$ be the center of circumcircle circumscribed to the triangle and $I$ the center of the inscribed circle. If $D$ is the point on the side $BC$ such that $OD$ is perpendicular to $BI$. Show that $ID$ is parallel to $AC$.
2017 missing
2018 Chile Level 1 P1
In the drawing, the five circles are tangent to each other and tangents to the lines $L_1$ and $L_2$ as shown in the following figure. The smallest of the circles has radius $8$ and the largest has radius $18$. Calculate the radius of the circle $C$.
In the drawing, the five circles are tangent to each other and tangents to the lines $L_1$ and $L_2$ as shown in the following figure. The smallest of the circles has radius $8$ and the largest has radius $18$. Calculate the radius of the circle $C$.
2018 Chile Level 1 P6
Consider two lines $L_1, L_2$ that are cut at point $O$ and $M$ is the bisector of the angle they form, as shown in the following figure. Points $A$ and $B$ are drawn in $M$ in such a way that $OA = 8$ and $OB = 15$ and the angle $\angle L_1OL_2$ measures $45^o$ . Calculate the shortest possible path length from $A$ to $B$ by touching lines $L_1$ and $L_2$.
In a triangle $ABC$, the medians $AM$ and $BN$ are drawn, Draw through $N$ a parallel to $BC$ and through $C$ a parallel to $BN$. These two lines intersect at $P$ and let $D$ be the midpoint of $PN$. Show that $CD$ is parallel to $MN$.
sources:Consider two lines $L_1, L_2$ that are cut at point $O$ and $M$ is the bisector of the angle they form, as shown in the following figure. Points $A$ and $B$ are drawn in $M$ in such a way that $OA = 8$ and $OB = 15$ and the angle $\angle L_1OL_2$ measures $45^o$ . Calculate the shortest possible path length from $A$ to $B$ by touching lines $L_1$ and $L_2$.
Consider a rectangle $ABCD$ with $| AB | > | BC |$ and let $E$ be the midpoint of $CD$ side. $F$ is chosen in $CD$ such that $| CF | = | BC |$. Suppose $AC \perp BE$. Prove that $| AB | = | BF |$.
www.olimpiadadematematica.cl
www.fmat.cl/index.php?showforum=540
http://inst-mat.utalca.cl/tem/tem/inicio/inicio1.htm
inst-mat.utalca.cl/tem/tem/inicio/pruebasolim/index.html












No comments:
Post a Comment