geometry problems from UQ/QAMT Problem Solving Competition, from University Of Queensland \ Queensland Association of Mathematics Teachers (Australia), with aops links
collected inside aops here
2002- 2016 (-14)
grade 8
The diagram below shows two circles, Circle $1$ and Circle $2$. The centre $C_1$ of Circle $1$ lies on the circumference of Circle $2$, and the centre $C_2$ of Circle 2 lies on the circumference of Circle $1$. The two circles intersect at points $A$ and $B$. The length of the line joining $C_1$ and $C_2$ is $2$ cm, rnd the length of the line joining $A$ and $B$ is $2\sqrt3$ cm. Find the area common to both circles (shaded).
A cube of side $3$ metres has three holes, each with a side of $1$ metres, running from the centre of one face to the centre of the opposite face. What is the total surface area of the solid in square metres?
Show how to place $12$ matches of unit length to form the perimeter of a single polygon to enclose exactly $4$ square units of area. No matches may be placed inside the polygon. No match may be broken, or placed on top of another match and each match must be laid end to end with other matches.
Suppose you have four rectangles of size $1\times 2$, three of size $2\times 3$, two of size $3\times 3$, and one of size $5\times 5$. Can you arrange them to form a single large rectangle?
In triangle $ABC$, angle $ABC$ is $120^o$. Point $D$ is chosen inside the triangle so that line $DA$ bisects angle $BAC$ and line $DC$ bisects angle $BCA$. What is the angle $ADC$?
Two vertical flag poles, $20$ and $80$ metres high, stand apart on a horizontal plane. Find the height of the point of intersection of the lines from the top of each pole to the foot of the other.
$ABCD$ is a square with side length $8$ cm. Circles are drawn with diameters $AB$ and $BC$, giving the diagram on the right. What is the area inside the square not covered by either of the circles?
$P$ is a point inside an equilateral triangle. The distances from $P$ to each of the sides are $5, 8$ and $19$. What is the height of the triangle?
A light hitting a mirror at angle $a$ measured from the perpendicular is reflected at angle $a$ on the other side of the perpendicular. The rough diagram here shows a cross section of the pentagonal prism found in some cameras, where sides $BC$ and $DE$ are mirrors and the angles $BCD$ and $CDE$ are equal. Light entering the prism is reflected twice, and emerges at $90^o$ to its original path. What is the angle$ BCD$?
An equiangular octagon has four sides of length $1$ and four sides of length $\sqrt{2}/2$, arranged so that no two consecutive sides have the same length. What is the area of the octagon?
A smaller square is placed inside a larger square. The sides of the two squares are parallel. If the areas marked are as shown, what is the area $A$?
Consider the star made by connecting $7$ points equally spaced around the circumference of a circle, as shown in the diagram. What is the interior angle of the heptagon?
A chessboard has squares of side length $1$ unit. A circle is drawn through the four corners of each black square and its interior coloured black (so each black square is covered up). What is the area of the remaining white space?
In the figure below the points are all $1$ unit apart. What is the area of the triangle $ABC$?
Suppose a parallelogram has corners $ABCD$, labelled clockwise (so $AB$ is parallel to $DC$). Let $P$ be a point inside the parallelogram with angles $\angle BAP = 42^o$ and $\angle CDP = 20^o$. What is the angle $\angle APD$?
grades 9-10
This four-pointed star is formed by taking a square with side lenght $1$ metre and joining the midpoints of each side to the corners as shown. What is the area of a star?
A belt is drawn tight around $3$ circles of radius $10$ cm, as shown. How long is the belt?
You have $7$ matches of equal length, $AX, XV, VZ, ZW, WY, YU$ and $UA$ laid out as in the diagram. Find the angle at $A$.
You have one rectangle of each of the following dimensions: $1 \times 18, 2 \times 16, 3 \times 13, 4 \times 11, 5 \times 10, 6 \times 9$ and $7 \times 7$. Is it possible to arrange them into a single large rectangle? Explain.
You lay out a $100$ m rope flat on the ground in a straight line, anchored at both ends. Now suppose you play out $1$ m of slack, so the $101$m rope is anchored at both ends, but can be lifted slightly off the ground at the $50$ m mark. How high can it be lifted?
In the rectangle $ABCD$ a triangle $AEF$ is drawn, where $E$ lies on $BC$ and $F$ lies on $CD$, and the triangles $ABE, ECF$ and $ADF$ all have the same area. What is the ratio $CF:FD$?
A square of area $20$ cm$^2$ fits inside a semicircle as shown. Find the area of the largest square that will fit inside the full circle.
$ABC$ is a triangle with $|AB| = |AC|$ and $\angle BAC = 20^o$. $E$ is a point on $AB$ with $\angle BCE = 50^o$ and $D$ is point on $AC$ with$ \angle CBD = 40^o$. What is the angle $\angle CED$?
Triangle $ABC$ is isosceles with $|AB| = |AC|$. $D$ is a point on $AC$ and $E, F$ are points on $AB$ with $|AE| = |ED| = |DF| =|FC| = |BC|$. What is the angle $ACE$?
A square and regular hexagon are drawn inside a unit circle as shown. What is the total area covered by the square and hexagon?
Triangle $ABC$ is isosceles with $|AB| = |AC|$. Points $D, E, F$ are drawn with $|AE| = |ED| = |DF| =|FC| = |BC|$. What is the angle $BAC$?
Consider a triangle $ABC$ with total area $26$ cm$^2$. Let $X$ be the midpoint of $BC$ and $Y$ be the midpoint of $AC$. Suppose $Z$ is chosen on the line $AB$ such that the area of $AZY$ is $9$ cm$^2$. What is the area of $XYZ$?
Two congruent non-overlapping equilateral triangles are placed wholly within a square of side length $1$. What is the maximum area they could cover?
A cone has radius $1$, height $6$. A cube just fits inside the cone, with the bottom of the cube level with the bottom of the cone. What is the volume of the cube?
Suppose we have six equally spaced points on a circle of radius $1$ unit. We connect one point to each of the other five with straight lines, as in the diagram. What is the product of the lengths of all these lines?
Suppose we have two concentric circles, as shown in the figure below. A chord of the outer circle has length $24$ m and is tangent to the inner circle. What is the area between the outer and inner circles?
Suppose we have two equilateral triangles, each with side length $1$, as shown below. For triangle (a), three circles of equal radius are drawn inside the triangle. Each circle is tangent tothe other two, and to two of the sides of the triangle. Triangle (b) also has three circles, the largest circle that can be drawn inside the triangle and two smaller circles with equal radii that are tangent to the large circle and to two sides of the triangle. Is the area covered by the circles bigger in (a) or (b), or are they the same? Find values for the areas and compare.
grades 11-12
You have a semicircle with diameter $AB$ of length $8$ cm, inside which are drawn non-overlapping semicircles of diameters $6$ cm and $2$ cm. A circle $C$ is drawn, touching all three semicircles as shown. Show that the perpendicular distance from the centre of this circle $C$ to the diameter $AB$ is equal to the diameter of the circle $C$.
Three spheres are just touching each other. The radii of the spheres are $1, 1$, and $2$ units. What is the area of the triangle joining the centres of the spheres?
Consider a rectangle with its vertices all on the boundary of a given triangle $T$. Let $d$ be the shortest diagonal for any such rectangle. Find the maximum value of: $$\frac{d^2}{Area \,\,T}$$over all triangles $T$
Three spherical melons, radius $9$ cm each, are placed on a flat table, each touching both the others. What is the radius of the largest orange that will sit on the table in the space between the $3$ melons?
In the diagram below, $FG + EG = DG$, $EG + DG = DA = 2EC = AF - FG$. Find the ratio $FC/EG$.
Connect all the vertices of a regular pentagon $ABCDE$ to each other with straight lines as shown. What is the ratio of the area of $ABCDE$ to the the smaller pentagon $PQRST$ ? You may use the fact that $\cos(36^o) =\frac{\sqrt5+1}{4}$ .
The Koch snowflake is constructed as follows. Start with an equilateral triangle of side length $1$. Now divide each side into $3$ equal parts and construct an equilateral triangle extending outwards on the middle section, and then delete its base. Repeatedly apply this subdivision step. The snowflake is the limiting shape obtained. What is its area?
The regular hexagon $ABCDEF$ shown below has area $1$. Find the area of the rectangle $BCEF$.
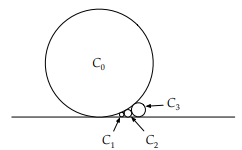
$C_0$ is a circle of radius $10$ metres tangent to the ground. $C_1$ is a circle of radius $1$ millimetre, external to $C_0$ and tangent to both $C_0$ and the ground. For $n > 2, C_n$ is a circle tangent to $C_0, C_{n-1}$ and the ground. The diagram to the right shows the first few circles in this pattern (not to scale).
How many circles can be placed in this way (before they get too large to be tangential to $C_0$)?
$AB$ is the diameter of a semicircle. $C$ is a point on the circle between $A$ and $B$. $D$ is another point on the circle between $C$ and $B$, with distances $|AC| = 9, |CD| = 2, |DB| = 12$. What is the length of the diameter $AB$?
Your semi-underground maths bunker has a $1$ metre square window, with the bottom side exactly at ground level, parallel to the ground. Suddenly a disc, $5$ metres in diameter, rolls past just outside the window at velocity $1$ m/s. For how long is at least part of your window obscured?
The great pyramid is a square based pyramid whose base square has side length $1$ and whose height is $3$, in some system of units. What is the radius of the largest sphere that will fit entirely within the pyramid?
The famous haberdasher’s problem involves cutting an equilateral triangle so that the pieces can be rearranged into a square. One solution is given in the following diagram:
Suppose the triangle has area $1$. What is the length of the longest cut in the triangle?
Three concentric circles of radii $1, 2, 3 $ respectively are drawn. An equilateral triangle is placed so that each of its vertices lies on a different circle, as shown. What is the side length of the triangle?
A triangle has internal angles $\alpha, \beta$ and $\gamma$ at vertices $A, B, C$ respectively. A point $P$ inside the triangle is such that $\angle BAP = \angle CBP = \angle ACP = 30^o$. What is the value of $ \frac{1}{\tan \alpha}+\frac{1}{\tan \beta }+\frac{1}{\tan \gamma}$ ?
Four equilateral triangles with side length $s$ are placed in a square of side length $1$, as shown. What is the value of $s$?
The volume of a spherical cap of height $h$ and base radius $a$, as shown in the figure below, is $\frac16 \pi h (3a^2 + h^2)$.
Suppose that a cylindrical hole is bored straight through the centre of a solid sphere and that the length of the interior wall of the hole is $8$ cm. What is the volume of the remaining part of the sphere?
Take a circle and inscribe $4$ non-overlapping equal sized circles $A, B, C, D$ such that $A$ is tangent to $B, B$ is tangent to $C, C$ is tangent to $D$ and $D$ is tangent to $A$ such that each is also tangent to the large circle. In each of these $4$ circles, inscribe $4$ smaller tangent circles in exactly the same way, to get $16$ small circles. Finally, inscribe a small circle $C_{17}$ in the space around the centre of the large circle and tangent to each of $A, B, C, D$. Which is larger, $C_{17}$ or one of the $16$ circles inside $A, B, C, D$?
Triangle $ABC$ is right angled at $B$. $P$ is a point on$ AB$ with $\angle BCP = \angle PCA$. $Q$ is a point on $BC$ with $\angle BAQ = \angle QAC$. If $AQ = 9$ and $CP = 8\sqrt2$, what is the length $AC$?

























No comments:
Post a Comment