geometry problems from Oral Moscow City Mathematical Olympiad for grades VI-VII with aops links in the names
Rectangles $ABCD$ and $KLMN$ have respectively parallel sides and are located as shown in the figure. Prove that the areas of the quadrangles $ALCN$ and $KBMD$ are equal.
Point $M$ is the midpoint of side $BC$ of triangle $ABC$. $CL$ is the perpendicular dropped from vertex $C$ on the line $AM$ ($L$ lies between $A$ and $M$). On the segment $AM$, the point $K$ is marked so that $AK =2LM$. Prove that $\angle BKM = \angle CAM$.
Oral Moscow MO 2019 VII p5
A rectangular sheet of paper was bent diagonally.
Can the perimeter the resulting pentagon turn out to be equal to the perimeter of the original sheet?
collected inside aops here
2005 - 2019,2021
it didn't take place in 2020
Oral Moscow MO 2005 VI p9
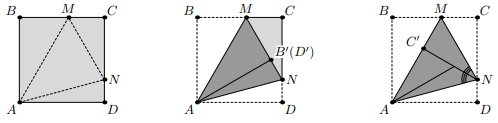
On the side $AB$ of the square $ABCD$ is marked an arbitrary point $M$. Prove that the area of the hatched triangle is the sum of the areas of the black triangles.
On the side $AB$ of the square $ABCD$ is marked an arbitrary point $M$. Prove that the area of the hatched triangle is the sum of the areas of the black triangles.
Cut a 5x5 square table into three parts with equal perimeters along the grid lines .
The maze consists of five circles (see figure). The lengths of the circles are $10, 20, 40, 80$ and $160$ meters. A person begins to walk along the labyrinth at a constant speed, who goes around all his circles clockwise in order of increasing lengths. Having passed the largest circle, he goes to the smallest and starts all over again. After a while, another person begins to walk through the maze, who walks at the same speed and according to the same plan as the first, but goes around all the circles counterclockwise. Prove that these two people will definitely meet.
[Лабиринт состоит из пяти окружностей (см. рисунок). Длины окружностей равны 10, 20, 40, 80 и 160 метров. По лабиринту с постоянной скоростью начинает ходить человек, который обходит все его окружности по часовой стрелке в порядке возрастания их длин. Пройдя самую большую окружность, он переходит на самую маленькую и начинает все сначала. Через некоторое время по лабиринту начинает ходить еще один человек, который ходит с той же скоростью и по тому же плану, что и первый, но обходит все окружности против часовой стрелки. Докажите, что эти два человека обязательно встретятся.]
it did not take place in 2007
Ivan Ivanovich built a blockhouse, square at the base, and is going to cover it with a roof. He chooses between two roofs of the same height: a gable and a four-pitched (see pictures). Which of these roofs will need more sheet metal?
[Иван Иванович построил сруб, квадратный в основании, и собирается покрывать его крышей. Он выбирает между двумя крышами одинаковой высоты: двускатной и четырехскатной (см. рисунки). На какую из этих крыш понадобится больше жести?]
Cut the shape in the picture into three equal parts (not necessarily along the grid lines).
(Equal are parts that can be combined by overlapping. The parts can be rotated and flipped.)
The sheet of paper has only one straight edge. The sheet was bent, then unbent back. $A$ is the common point of a straight edge and a fold line. Construct a perpendicular to this line at point $A$. Do this without drawing tools, but only by bending the paper.
[У листа бумаги только один ровный край. Лист согнули, потом разогнули обратно. А — общая точка ровного края и линии сгиба. Постройте перпендикуляр к этой линии в точке А. Сделайте это без помощи чертёжных инструментов, а лишь перегибая бумагу.]
There was a fly in each vertice of the cube. Then all the flies took off at once and landed, one at each peak, in some other order. Prove that there are three flies that, in the initial and final positions, sat at the vertices of equal triangles.
Petya cut a scalene triangle out of plastic. Show how it is possible, using only this tool as a template, to construct the bisector of some angle of the triangle.
[Петя вырезал из пластмассы неравносторонний треугольник. Покажите, каким образом можно, пользуясь только этим инструментом как шаблоном, построить биссектрису какого-нибудь угла треугольника, равного вырезанному.]
In triangle $ABC$ on the side $AB$, point $K$ is selected and the bisector $KE$ of triangle $AKC$ and the altitude $KH$ of triangle $BKC$ are drawn. It turned out that the angle $EKH$ is right. Calculate $BC$ if $HC = 5$.
In triangle $ABC$, the bisector of angle $C$ intersects side $AB$ at point $M$, and the bisector of angle $A$ intersects the segment $CM$ at point $T$. It turned out that the segments $CM$ and $AT$ have divided the triangle $ABC$ into three isosceles triangles. Find angles of triangle $ABC$.
A straight line is drawn through point $Y$ on side $AB$ of an equilateral triangle $ABC$ that intersects side$ BC$ at point $Z$, and the extension of side $CA$ beyond the point $A$ at point $X$. It is known that $XY = YZ$ and $AY = BZ$. Prove that straight lines $XZ$ and $BC$ are perpendicular.
From a square sheet of paper folded triangle (see pictures). Find the marked angle.
The bisectors of triangle $ABC$ meet at point $I$, $\angle ABC = 120^o$. Points $P$ and $Q$ are marked on the extensions of sides $AB$ and $CB$ beyond point $B$, respectively, so that $AP = CQ = AC$. Prove that $PIQ$ is a right angle.
Two corners of a rectangular sheet folded as shown in the illustration. The opposite side was thus divided into three equal parts. Prove that the filled triangle is equilateral.
The paper equilateral triangle was bent in a straight line so that one of the vertices fell on the opposite side (see figure). Prove that the angles of the two white triangles are respectively equal.
On a grid of equilateral traces of squares the angle $ACB$ is constructed (see the figure). Find its value.
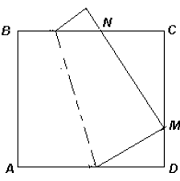
Squares $ABCD$ and $BEFG$ are arranged as shown in the figure. It turned out that points $A, G$ and $E$ lie on one straight line. Prove that then points $D, F$ and $E$ also lie on one straight line.
Two square carpets were brought to a large square hall, the side of one carpet is double than the side of the other. When they were placed in opposite corners of the hall, they cover a common area of $4$ m$^2$ , and when they were placed in adjacent corners, they cover a common area of $14$ m$^2$. What is the size of the hall?
Oral Moscow MO 2017 VII p6 (Saint Petersburg MO 2010 10.3)
$M,N$ are midpoints of $AB$ and $CD$ for convex quadrilateral $ABCD$. Points $X$ and $Y$ are on $ AD$ and $BC$ and $XD=3AX,YC=3BY$. $\angle MXA=\angle MYB = 90$. Prove that $\angle XMN=\angle ABC$
Folklore
A rectangular sheet of paper was bent diagonally.
Can the perimeter the resulting pentagon turn out to be equal to the perimeter of the original sheet?
Folklore (edited by A. Peshnin)
Oral Moscow MO 2019 VII p8
Inside the triangle $ABC$, point $P$ is marked so that the sum of the angles $ABC$ and $APC$ equals $180^o$ and $CP = AB$. Prove that $\angle CAP <60^o$
Inside the triangle $ABC$, point $P$ is marked so that the sum of the angles $ABC$ and $APC$ equals $180^o$ and $CP = AB$. Prove that $\angle CAP <60^o$
(A. Peshnin)
Six sticks are such that any three can create a triangle. Is it necessary from them to make the perimeter of a triangle, in which one side consists of one stick, the second consists of two sticks, and the third consists of three?
Is there a regular hexagon with vertices at the nodes of a checkered lattice, which can be cut into regular octagons, the vertices of which are also located at the nodes of the lattice?
Points $E$ and $F$ are marked on sides $BC$ and $CD$ of square $ABCD$, respectively, so that $AEF$ is an equilateral triangle. Point $M$ is the midpoint of segment $AE$. Prove that $CM = AB$.
The checkered square is divided into several cells in shapes of rectangles. Not all rectangles are equal to each other, but all are equal perimeter. Find the smallest possible square size.
A perpendicular bisector of a side of an acute angle triangle divides one of its altitudes in the ratio $2 : 1$, counting from the top. Find one of the angles of the triangle.
The paper square $ABCD$ is folded along a straight line so that that the vertex $A$ coincides with the interior point $M$ of the side $CD$, and side $AB$ (in the new position) crosses side $BC$ at point $N$ (see figure). Find the angle $\angle MAN$.
source: olympiads.mccme.ru/ustn/
No comments:
Post a Comment